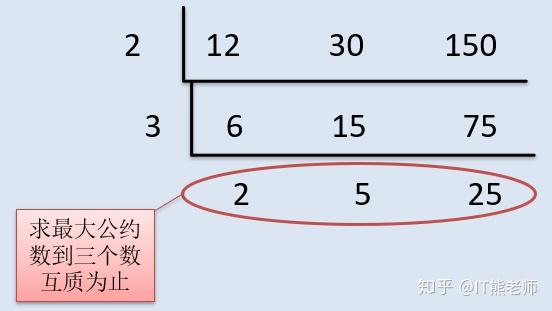
以上と、素因数分解を使う事で「 最大公約数も約数も公約数もすべて求められる 」という事です。 そして「 負の指数 」という概念もとても便利なものでした。これはまた大きな武器になりそうです。 次回で素因数分解 3 部作の完結です 。最も一般的な解き方は、3つ全ての数を割る事ができる共通因数で割っていき、割った数をすべて掛けると最大公約数になります。 それが以下の画像1枚目で、24,56,84は2で割れる、12,28,42も2で割れるので、2×2で最大公約数は4です。 (一の位が偶数だと、必ず2で割れます) 他の解き方(以下の 2最大公約数の約数を列挙する AtCoder 版!マスター・オブ・整数 (素因数分解編) Qiita この記事によると 二つの整数 a,b の公約数は、a,b の最大公約数の約数である。 とのこと。 つまり、 2つの整数の最大公約数を求めて;

Python使用更相减损术计算两个整数的最大公约数 快资讯
最大公約数 求める 素因数分解
最大公約数 求める 素因数分解-最大公約数とは,公約数のうち最大のもの。 最小公倍数とは,公倍数のうち最小のもの。 高校の教科書では,最大公約数を求める場合,2 つの整数をそれぞれ素因数分解し, その指数の小さい方を掛け合わせて求めます。また,最小公倍数を求める場合は共通の約数(=公約数) 1 , 2 , 3 , 6 の中で最大のものは 6 ⇒ 最大公約数は 6 間違って「最小公約数」などと言わないように.最小公約数は,計算しなくても1に決まっているので「最小公約数」などという用語は使わない.(=当たり前でつまらないことだから)




求两个数的最大公约数和最小公倍数 Maniac Ran的博客 Csdn博客
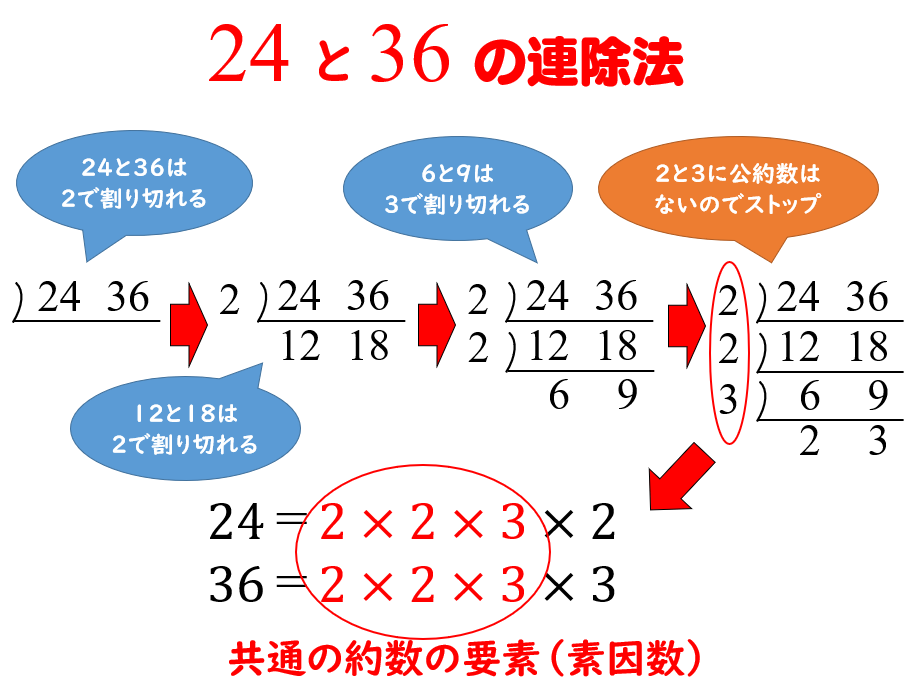
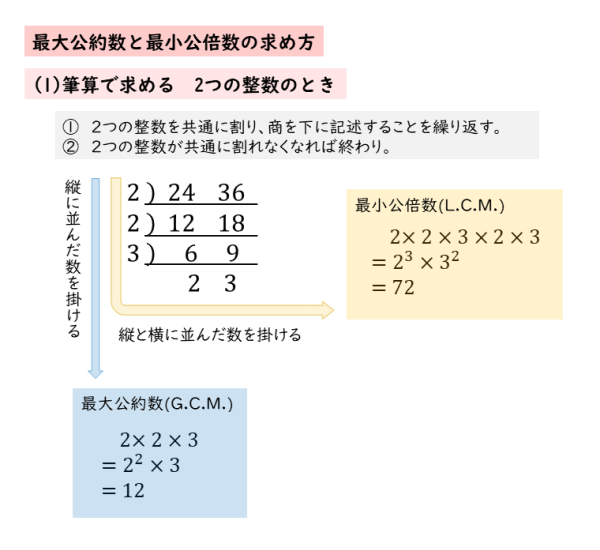
例えば12と18の、 最大公約数 と 最小公倍数 を求める方法として、 連除法 ( はしご算 )と呼ばれる方法があります(単に 素因数分解 ということもあります)。2 最大公約数の求め方 最大公約数の求め方を復習す る。 ・約数をすべて並べて求める。 ・素因数分解を用いて求める。 ・ユークリッドの互除法を用い て求める。 最大公約数の最適な解法 〇それぞれの解法のよさを認識 する。 ・交流活動を行う。素因数分解を使って,約数や最大 公約数を求めようとしている。 素数と素因数分解を活用した問 題解決の過程をふり返って検討 しようとしている。 ② 素因数分解の活用 ・素因数分解を利用した自然数の約数の求め方を考えること ・素因数分解を利用し
素因数分解と公約数・公倍数をマスターすれば、分数の約分・通分は楽勝です。 分数を暗算でガンガン解くことができます。 公約数と公倍数の学習マニュアルはこんな感じ。 最大公約数ドリル ①小さな数で大きな数を割る 4:12 12÷4=3 割り切れるので4中3 素数·素因数分解 最大公約数·最小公倍数(2) 問題7、問題8、問題9、問題10のhelp 間違っている =>作者: 連絡ありがとう.めったにない変わったエラーでした・・・指数(肩に付ける小さい数字)が地上に降りていましたので訂正しました.数学の問題を入力 解 代数 三角法 統計 微積分 行列 変数 リスト
素因数分解を行い、最大公約数を求める方法もあります。素因数分解の詳細は、下記が参考になります。 素因数分解とは?1分でわかる意味、素数、約数との関係 16と40の素因数分解を行います。 16 ⇒ 2×2×2×2=2 3 ×2 40 ⇒ 2×2×2×5=2 3 ×5 最大公約数は、それぞれの数値を素因数分解し、共通する素因数をすべて掛けることによって求められます。たとえば、12=2×2×3で、30=2×3×5なので、最大公約数は2×3=6となります。 関連する関数 lcm 最小公倍数を求める 素因数分解で約数の数(個数)だけでなく・個々の約数も求められる 最大公約数は、 いくつかの数の共通の約数のうち最大の数 です。 28と42であれば、上記のように、 共通の約数(公約数)が「1、2、7、14」と4つあり、 最大の公約数は14ですので、 28と



Excel Gcd函数的使用方法 百度经验



Excel运用gcd求多个整数的最大公约数 百度经验
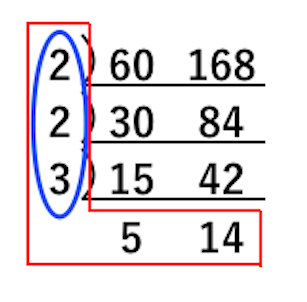
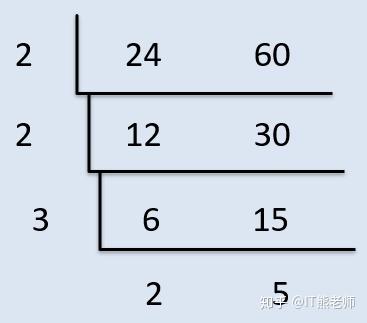
この年齢になって、ちょっと恥ずかしいのですが素因数分解について質問があります。なぜ素因数分解で「最小公倍数」や「最大公約数」がわかるのでしょうか?最大公約数の場合、例えば8と12だと 2)8 12 ーーーーーー 2)4〈最大公約数〉 すべての数に共通な素因数でわることを,共通な素因数 がなくなるまで繰り返す。すべての数に共通な素因数の 積が最大公約数となる。 2) 24 180 2) 12 90 3) 6 45 2 15 ・36と60と126の最大公約数,最小公倍数を求める。それぞれの素因数を暗算で見つけられる人は少ないと思う。 素因数分解を行わず、一般の数に適用可能なアルゴリズムとして、ユークリッドの互除法がある。 例.851と437の最大公約数を求める。 最大公約数をdとする。もちろん、1かもしれない。



Noi2 2 7592求最大公约数问题 循环结构 Oier博客




19 02 27 Gcd 递归求最大公约数 简书
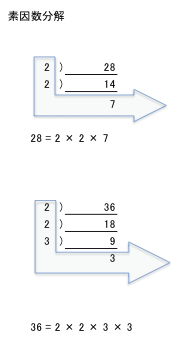
例えば、 2⋅ 33 ⋅72 2 ⋅ 3 3 ⋅ 7 2 と 23 ⋅ 5⋅ 72 2 3 ⋅ 5 ⋅ 7 2 (2646 と 1960) の最大公約数であれば、各素因数の小さい方をとっていって、 21 ⋅ 30 ⋅50 ⋅72 = 98 2 1 ⋅ 3 0 ⋅ 5 0 ⋅ 7 2 = 98 と求められます。最大公約数や最小公倍数を求めるには,素因数分解を使う.例えば,42と60をそれぞれ素因数分解すると \begin{align} 42&=2\cdot3\cdot7\\ 60&=2^2\cdot3\cdot5 \end{align} となる.よって、24と30の最大公約数は6です。 最大公約数の求め方は「素因数分解 ⇒ 共通する因数を抜き出す ⇒ 積を求める」だけなので、機械的に計算できます。 まずは素因数分解を勉強しましょう。最大公約数の求め方は下記も参考になります。




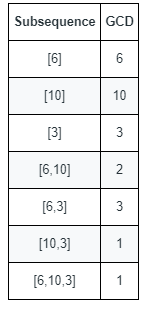
3つの数の素因数分解で最大公約数と最大公倍数を求める問題なのですが これってどこが間 Clear




Python使用更相减损术计算两个整数的最大公约数 快资讯
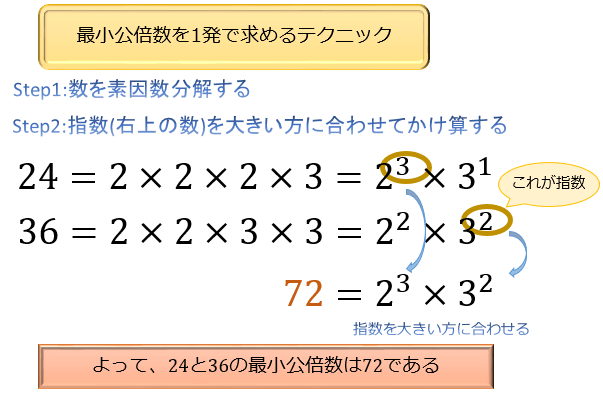
素因数分解することによって,その数の約数や最小公倍数,最大公約数を求めることができます。 例えば,84の約数は,1,2,3,7,2 2 2 2 2 2 2 2 しかし,小学校では,約数や倍数を分数の計算に用いることに主眼がおかれるので,素因数分解に基づく形式的Pythonで最大公約数と最小公倍数を算出・取得 notenkmkme Pythonで素因数分解(試し割り法) NumPyで最大公約数・最小公倍数を算出・取得 Pythonで階乗、順列・組み合わせを計算、生成 Python, complex型で複素数を扱う(絶対値、偏角、極座標変換など) Pythonで指数関数・対数関数を Q FFTにおけるゼロそこで、最大公約数の探し方のコツをおさえておこう。 ある2つの数(3つ以上の数)の最大公約数を求めるときには、まず、それらの数を 素因数分解 しよう。 でてきた素因数を見比べて、 指数が小さい方を選んでかけ算する と最大公約数になるんだ。




欧几里得算法求最大公约数 Gcd 的数学原理 於清樂 博客园



如何计算最大公约数 百度经验
を素因数分解すると, =3*52 したがって,0の約数は,1,2,4,5,8,10,,25,40,50,100,0 最大公約数の求め方 問3次のように,素因数分解を利用して,36と90の最大公約数を求めました。 にあてはまるも のを書き入れましょう。最大公約数を求める計算機 留意事項 最大公約数 (GCD)を簡単に求める計算プログラムです エクセルじゃないですが、最大5つの数に対して計算可能です 入力値は最大5桁までの整数に限ります(負荷の関係で適当に制限かけてます) 入力値が「0」の場合は4 素因数分解と約数・倍数 ⑴ 次の数の約数をすべて求めなさい。 ① ② 63 ③ 245 〔 〕 〔 〕 〔 〕 ⑵ 102 にできるだけ小さい自然数をかけて,その結果を 70 の倍数にしたい。どんな数をかければよいですか。 〔 〕 5 最大公約数・最小公倍数




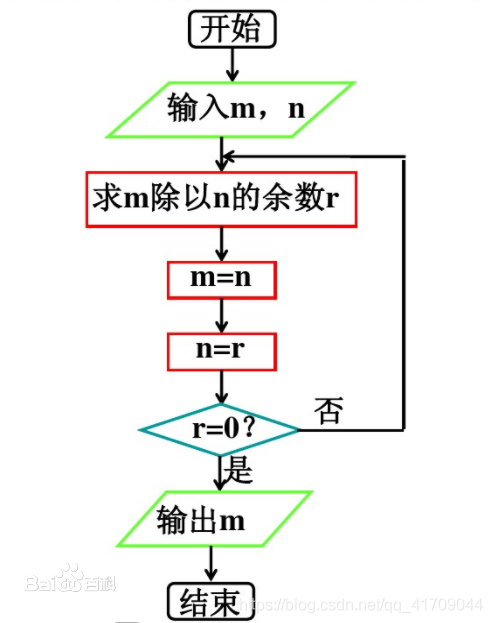
辗转相除法 求最大公约数 欧几里得算法 Extgcd 算法提高求最大公约数 Gcd And Lcm 合数分解 Claire的博客 Csdn博客 最大公约数欧几里得算法



Lcd和gcd函数 最小公倍数 最大公约数的求法 百度经验
公約数 計算機 計算機は、次を使用して、指定された数の最大公約数を計算する効率的な 公約数 計算機 ファインダーです。 要因リストメソッド; 3 最大公約数の3つの求め方 31 最大公約数の求め方その1:地道にやる 32 最大公約数の求め方その2:筆算 33 最大公約数の求め方その3:素因数分解 4 数が3つのときの最大公約数の求め方 5 最大公約数の練習問題 6 おわりに:最大公約数を求めるときはA 素因数分解を利用した最大公約数や最小公倍数の求め方を十分に理解している。 b 素因数分解を利用した最大公約数や最小公倍数の求め方を理解している。 a 素因数分解を利用して,最大公約数や最小公倍数を手際よく求めることができる。



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学
素因数分解 素因数である可能性のある数をforで回してひたすら求めます。 ここでは簡単のためにやりませんが、 2, 3, 5, 7, と2以外は奇数を数えたほうが少し高速化されます。 「1」×「その数自身」でしか表せない「数」があります このような数のことを「素数(そすう)」といいます 次に素因数分解とは「自然数」を「素数」だけの積の形( × )で表すことです この「素因数分解」を使う問題を一緒に見ていきましょう 前半(最大公約数・最小公倍数問題)解答・解説 方針1素因数分解もどきの利用 限られた時間のなかで効率よく解くには、素因数に完全に分解しないほうがおそらく簡単です。 解



辗转相除法 Gcd 求最大公约数 Yanfive 程序员宅基地 Gcd辗转相除法 程序员宅基地




怎样求两个数的最大公约数 百度经验
2.最大公約数の計算1 それでは、40と30の最大公約数を求めてみましょう。 まず初めに行う作業は、40と30をそれぞれ素因数分解します。 素因数分解とは、ある数を素数の積で表した形のことをいまず,最大公約数を次のいずれかの方法で求める. i 共通に割れるだけ割っていく方法 ii 素因数分解を利用して共通な指数を探す方法 iii ユークリッド互除法による方法 iiiでは最小公倍数を求める方法も示されるが,iiiのように最大公約数だけが求まるときは,次の関係式 ab=gl を用いユークリッドの互除法最大公約数の計算ユークリッドの互除法とは, 2つの整数に対して, その最大公約数を計算するときに使う方法です 最大公約数は, 通常は素因数分解を用いて次のように求めます 例として, 16 と 210 の最大公約数を考えます\begin{align*} 16 &= 2^5 \times




最高最大公約数小学生
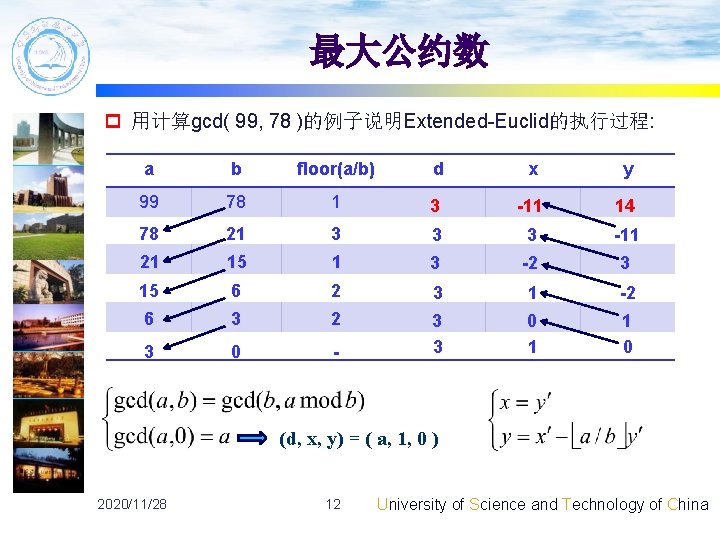



1128 4 University Of Science And Technology Of
ディズニー! 邦ロック! 仕事は事務! 介護! 美容! 自分はちょいぽちゃだけど細身で高身長な方がいいです! 恥ずかしがり屋なので積極的な方がいいです! 今までさんざん遊んできたけどそろそろ年齢的に落ち着いた恋愛がしたいです! あとなんかある? 自然数の素因数分解が一意的であることを証明しよう。前回の考察から、一意分解条件を示すには次の2つの条件: (Ⅱ)約鎖条件 (Ⅲ)素元条件 を満足することを確認すればよい。ここではこの2つを確認しよう。 ただし(Ⅲ)素元条件については、「最大公約数の2つの定義について、両素因数分解を活用して、これらの最大公約数、最小公倍数を求めてみましょう。 (1)\(60, \ 72\) をそれぞれ素因数分解をします。 最大公約数とは、それぞれの共通する素因数をすべて取り出して掛け合わせた数。



Gcd Lcm计算器 最大公约数lcm安卓下载 安卓版apk 免费下载



Leetcode 1819 序列中不同最大公约数的数目 Acwing
ある2つの数の最大公約数を求めるとき、これまではそれぞれの数を素因数分解して求めてきたね。でも、例えば 「722と171の最大公約数は?」 などのように 大きい数の最大公約数 をたずねられると、それぞれの数を素因数分解するのはちょっと骨が折れそうだ。最大公約数と最小公倍数 素因数分解 一次方程式の解 二次方程式の解 三次方程式の解 四次方程式の解 一次不等式の解 二次不等式の解 三次不等式の解 四次不等式の解 二元連立方程式 n次方程式の解



最大公約数と最小公倍数のひみつ 苦手な数学を簡単に




Excel最大公约数最小公倍数函数gcd和lcm 每日头条



プログラミング 素因数分解と最大公約数 Youtube



Noip知识点 最大公约数和最小公倍数 知乎




寒假培训 Gcd 最大公约数 Lcm 最小公倍数 Ssnti的博客 Csdn博客



Excel最小公倍数和excel最大公约数计算方法 Gcd函数和lcm函数




数学扫盲 辗转相除 只布布倩 Csdn博客




如何找出两个整数的最大公因数




如何找出两个整数的最大公因数




五年级奥林匹克数学第25讲最大公约数下载 Word模板 爱问共享资料



公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun




第1回 Pythonで最大公約数と最小公倍数のプログラムを書いた 疑念は探究の動機であり 探究の唯一の目的は信念の確定である




Binarysearch 最小公倍数 最大公约数的应用0072 Youtube



1



最大公約数と最小公倍数




小知识 什么是 欧几里得算法 Mb5fe18fab305a5的博客 51cto博客



最大公约数 快懂百科
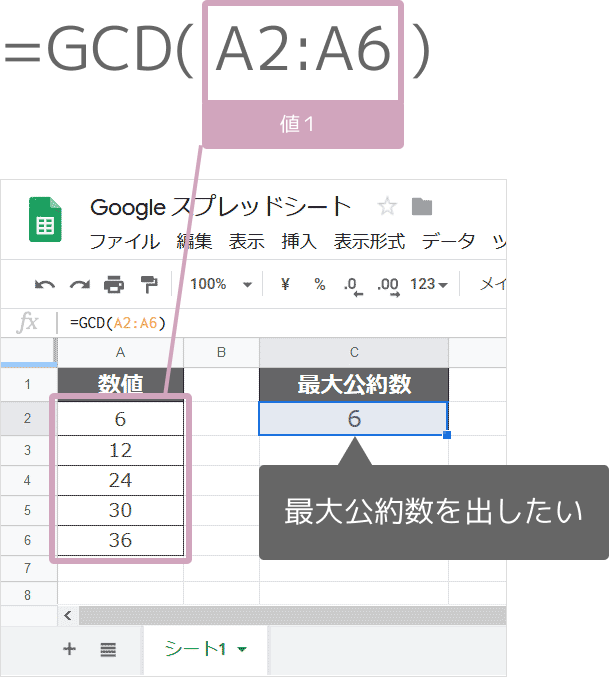



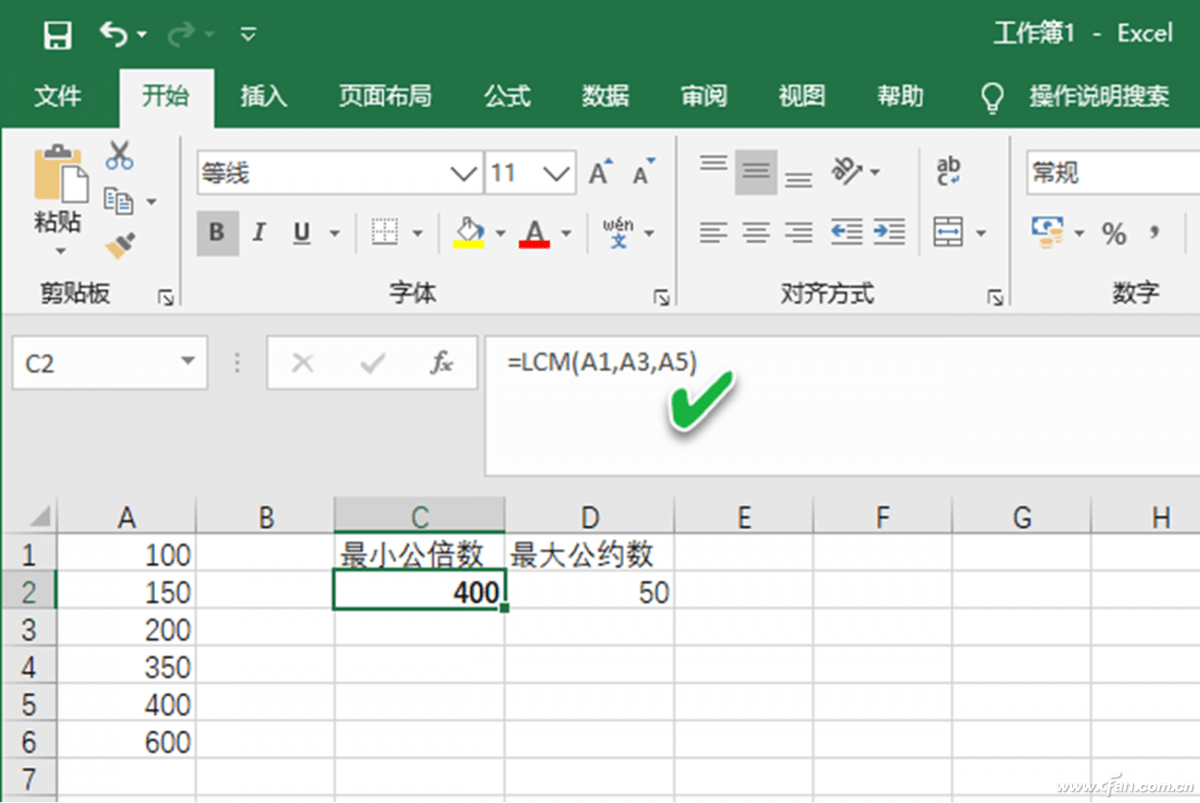
最大公約数を求めるgcd関数 スプレッドシートの使い方



C语言求解最大公约数之gcd欧几里得算法 哔哩哔哩 つロ干杯 Bilibili




最大公約数と最小公倍数を求める 2 3 素因数分解を利用する 自由研究ノート 仮



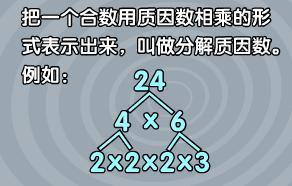
怎样分解质因数 怎样分解质因数 篆体字转换器



最大公約数と最小公倍数
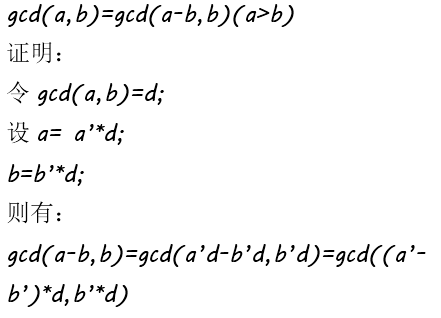



19中山纪念中学夏令营 Day19 数论初步 Gcd 最大公约数 素数相关 Xyyxp 博客园




C语言2个数度最大公约数与最小公倍数 每日头条




最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 養成講座



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




用python求最大公约数与最小公倍数 简书




最大公約数と最小公倍数を求める 1 3 割れるだけ割ってみる 自由研究ノート 仮




最大公约数和最小公倍数 牛客博客
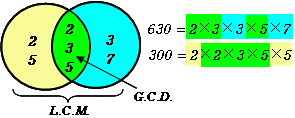



最大公約数と最小公倍数 高精度計算サイト




整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




A024 最大公因數 Gcd 和平高中特色課程 C C 程式設計




求两个数的最大公约数和最小公倍数 Maniac Ran的博客 Csdn博客




四 最大公约数 裴蜀定理 扩欧 Lonely Pinna的博客 Csdn博客



最小公倍数って何 その求め方と素因数分解のテクニック アタリマエ




机试小课堂丨c 数论 不仅漂亮 其实也有大用处 知乎




欧几里得拓展算法求模逆元 幸福诗歌的博客 程序员宅基地 程序员宅基地




行测计算题常用办法 约数与倍数



42和36最大的公因数42和36最大的公因数是多少 天奇生活




最大公约数gcd与最小公倍数lcm Fishers 博客园



Verilog 求最大公约数 Gcd Mcev0y的博客 程序员宅基地 Verilog 最大公约数 程序员宅基地




Noip知识点 最大公约数和最小公倍数 知乎



最小公倍数の求め方や性質を全て解説 実際の入試問題の解説付き Studyplus スタディプラス



办公小技巧 快速求取excel最小公倍数或最大公约数 函数



素因数分解と最大公約数 最小公倍数 Gamesprit




五年级最大公约数的概念以及练习题 宝宝学习网



1
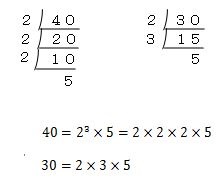



最大公約数の求め方 もう一度やり直しの算数 数学




在主要因素中分解 提示 21



Noip知识点 最大公约数和最小公倍数 知乎




最大公約数と最小公倍数を求める 2 3 素因数分解を利用する 自由研究ノート 仮




Excel函数gcd实例一 计算最大公约数 百度经验



请问求最大公约数和最小公倍数的程序如何理解 知乎




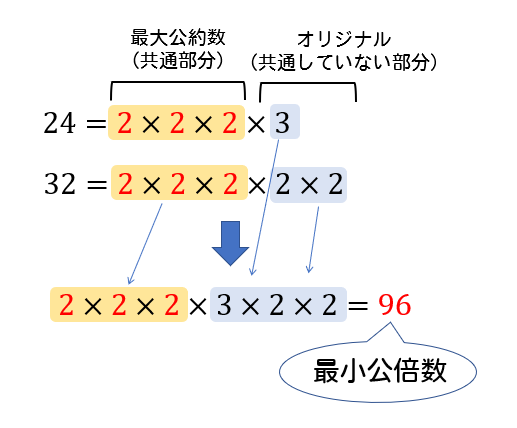
24と32の最大公約数と最小公倍数 Irohabook




如何找出两个整数的最大公因数




小知识 什么是 欧几里得算法 华为云



最小公倍数 最大公約数の求め方はこれでいいんですか 素因数分解は Yahoo 知恵袋




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




最大公约数 简书




公约数 搜狗百科




如何求解最大公约数和最小公倍数 公众号 猴子数据分析 Csdn博客 最大公约数怎么求算法




最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場



万里acm Discuss3



最大公约数 搜狗百科



1




高1です 数学がわかりません 教えてください 最大公約数と最小公 その他 学校 勉強 教えて Goo
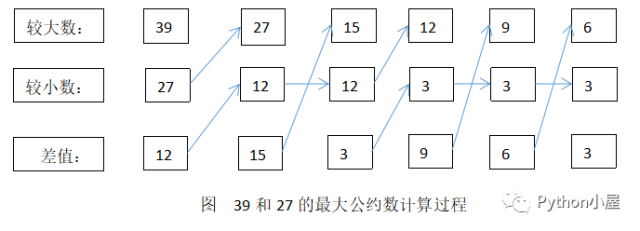



用python求最大公约数 Python使用更相减损术计算两个整数的最大公约数 简明教程




は36 108 Clear



2つの整数の最大公約数 最小公倍数と 3つの整数の最大公 Yahoo 知恵袋




最大公约数 Greatest Common Divisor 牛客博客




Excel 如何利用gcd函数实现计算最大公约数与最小公倍数 Office教程网
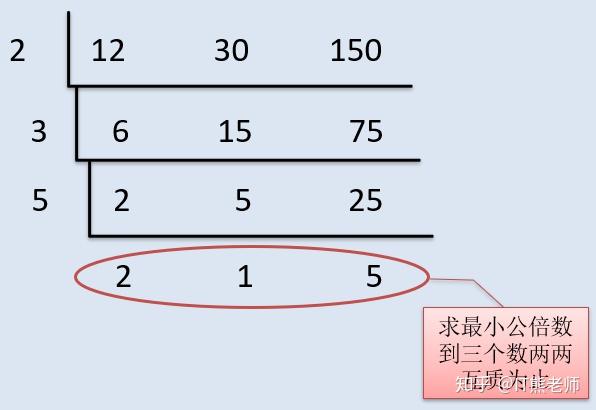



Noip知识点 最大公约数和最小公倍数 知乎
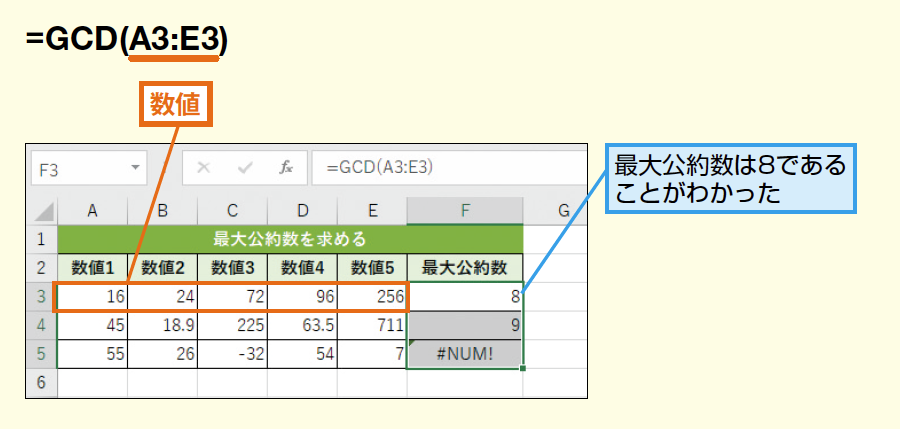



Gcd関数で最大公約数を求める Excel関数 できるネット



16年公务员考试行测答题技巧 最小公倍数和最大公约数步知行测 移动版
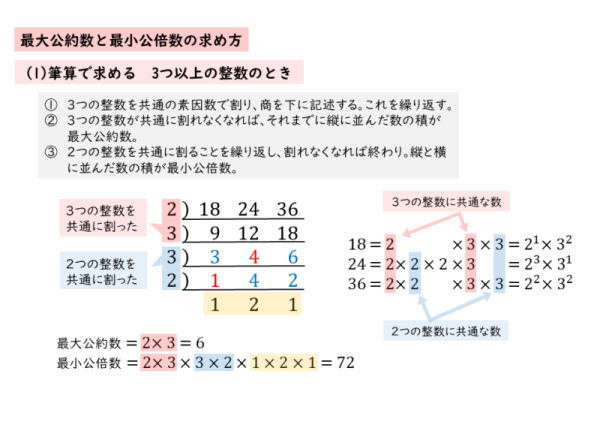



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




如何找出两个整数的最大公因数




蓝桥杯 最小公倍数和最大公约数 It S The Climb 程序员宅基地 程序员宅基地
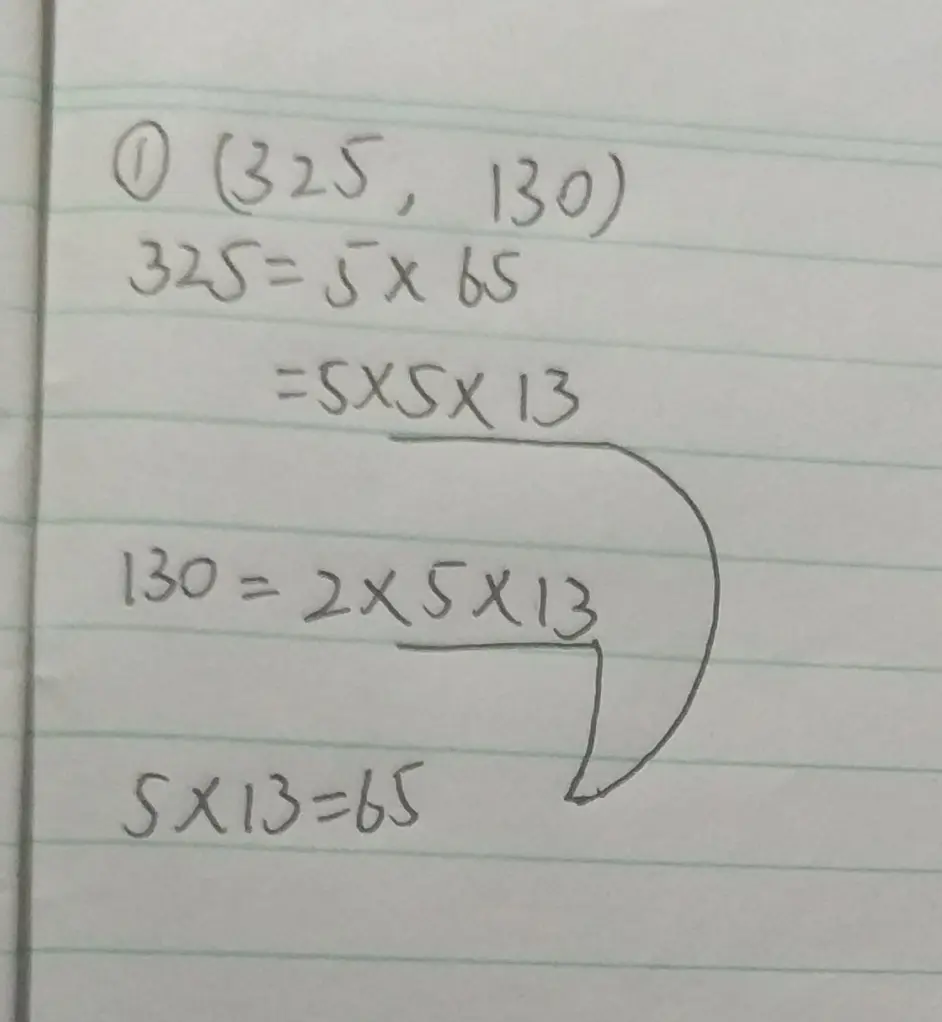



小学的求最大公约数还能玩出这么多花样 哔哩哔哩




C语言 求n个数的最大公约数和最小公倍数 Blaxqk的博客 程序员宅基地 求n个数的最大公约数c语言 程序员宅基地




辗转相除法 更相减损法 Stein算法 Csdn文章已停止维护 后续文章会在https Blog Hufeifei Cn 持续更新 Csdn博客 更相减损法




质数 最小公倍数 最大公约数 简书
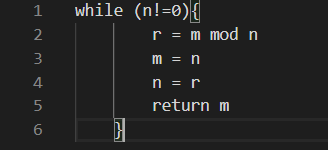



算法入门 一 求最大公约数 欧几里得游戏 带锁的门 Lamplight 博客园



C语言求最大公约数 C语言中文网




什么是最大公约数 什么是最小公约数 展天联盟



最小公倍数とは 求め方や計算問題 最大公約数との関係 受験辞典



0 件のコメント:
コメントを投稿