== 相似図形,平行線と比 == ※ 問題数は4題ではありません.合計13題あります. 問題1 _____ 第1問 / 全3問中 採点する 解説 次の問題 問題2 _____ 第1問 / 全3問中 採点する 解説 次の問題 問題3 _____ 第1問 / 全3問中 採点する 解説 次の問題 問題4 _____ 第1問 / 全3問中 採点わるとき,それぞれの交点は,その2辺を等 「平行線と比」の定理を説明させる。 相 しい比に分けることを考えさせる。 似 10 「平行線と比」の定理を利用して,線分 課題把握,解決の見通しや確認を 平行線と線分の比へ。 来週は中点連結定理や 角の二等分線の性質を学び、 次は面積や体積の計量に 入ってゆきます。 ペースとしてはかなり上々。 昨年は11月過ぎくらいに やっていた内容ですからね。 夏休みは短くなって

平行線と線分の比 06 平行線と比の発展問題 その2 Youtube
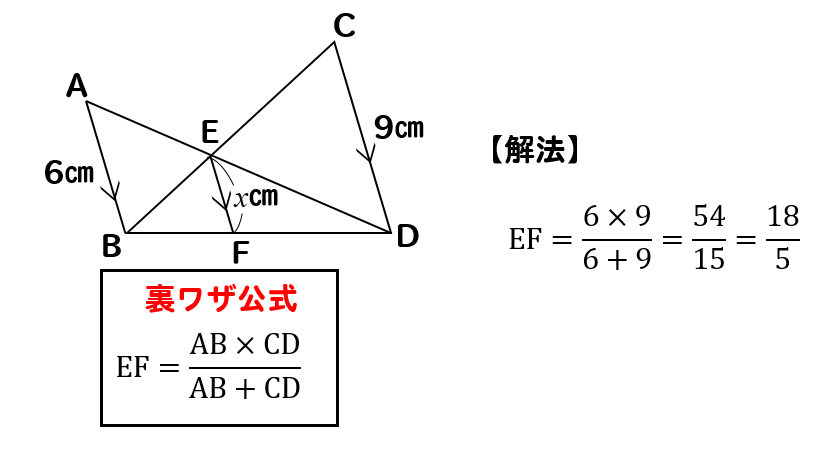
平行線と線分の比 裏ワザ
平行線と線分の比 裏ワザ-平行線と線分の比 6 0 0 Loading (view fulltext now)5/5時 ねらい ・ 「線分の比と平行線」が「平行線と線分の比」の逆になっていることを理解する。 ・ 線分の比と平行線の性質を利用して、問題を解決することができる。 段階 学習活動 数学的活動を通した指導のポイント ( は数学的活動をともなう学習活動) つかむ 本時の学習内容「線分の比と平行線の性質を利用して、問題を解決しよう」を知る。
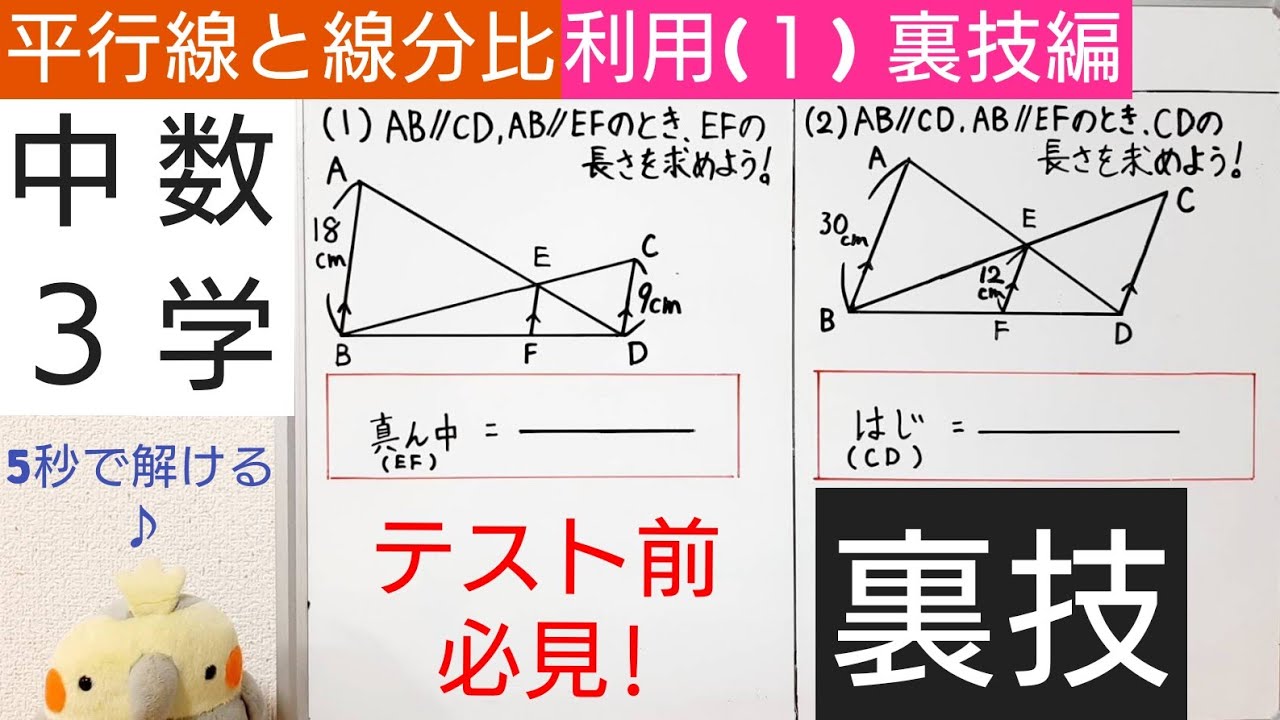



中3数学 15 平行線と線分の比の利用 1 裏技 Youtube
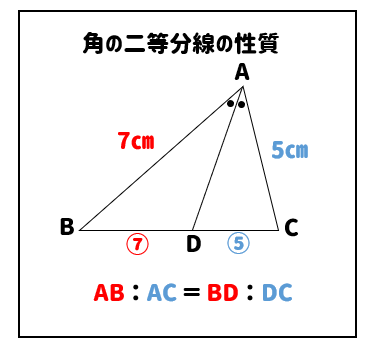
角の二等分線と線分の比 a b c d abcで、∠bacの二等分線と辺bcとの交点をdとすると、 abac=bddcとなる。 証明 点cを通り、adに平行な直線を引き、baの延長との交点をeとする。 ad//ecより平行線の同位角は等しいので∠bad=∠aec(1) 平行線の錯角は等しいので∠dac=∠ace(2)中学3年生 平行線と線分の比、基本編、応用編、中点連結定理編 みなさん、初めまして。 本講座を担当している葉一(はいち)と申します。 私は元塾講師なのですが、#平行線 #相似 #線分比 今回は、相似の3回目。平行線と線分比を学びます。解説のとおりにすれば、どんな問題も簡単に解けます。例題でわかり
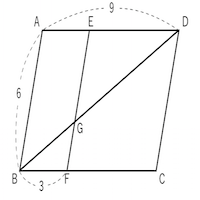
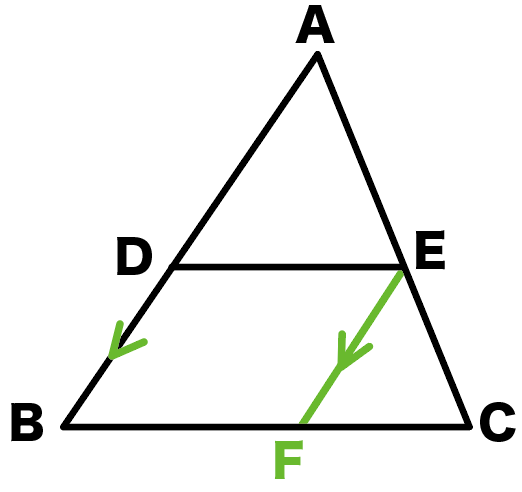
まずはどこに平行線を引くか考えますよね? まずはADDBが2:1であることに注目して緑線の補助線を引きます。 すると、、、 緑線とAEの交点からAまでとEまでの比は2:1になります。 そして線分CDに注目するために2:1を4:2にすることでCE:EXは5:2となりま す よってCFFDは5:2となります。 ここで学んでほしいのは 補助線の使い方 です。 問題をみてどこに補助線て線分の長さを求めることができる。 (ノート・振り返り) 平行線と比の定理を利用して,図形の性質 を証明することができる。 平行線と比の関係を使って課題解決しよ うとしている。 3 相 似 な 図 形 の ・相似比と面積比の 関係を見つける。 (1)相似と線分比2 addb=34, eはbcの中点である。 affeを求めよ。 a b c d e f aを通り、bcに平行な直線と、cdの延長線との交点をpと
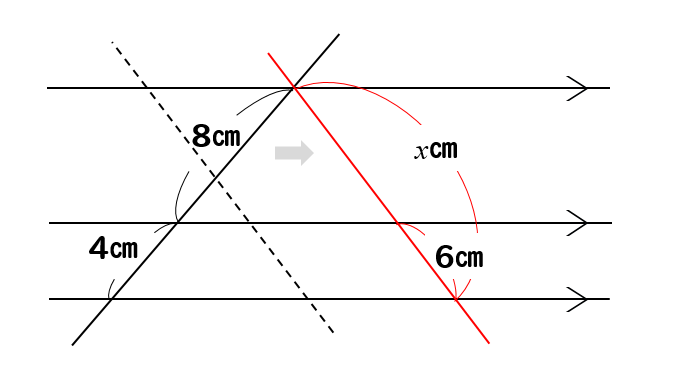
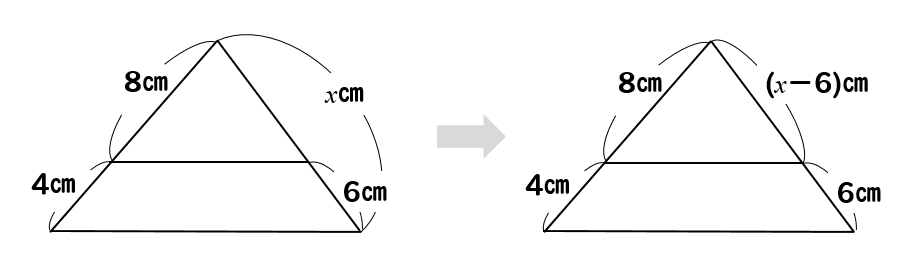
の相似条件、平行線と 線分の比についての性 質、相似比と面積比及 び体積比の関係などを 理解し,知識を身に付 けている。 8 指導計画(全時間 本時第8時) 学 習 内 容 (時数) 評価の観点 評価規準 評価方法 相似な 図形 ・図形の相似の意味や相似比について 理解し,相似な図形の性質を平行線と線分の比 右図2のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. bd//ce のとき まず図1の(1)が成り立つ. 前に習っているから,ここでは復習になるが一応証明しておくと次のように・ 「線分の比と平行線」が「平行線と線分の比」の逆になっていることを理解する。 ・ 線分の比と平行線の性質を利用して、問題を解決することができる。




2直線の交点 の裏技解法を知ろう 3パターンの解法
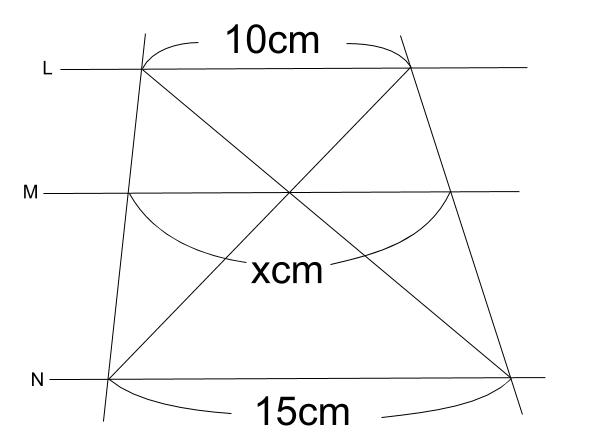



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
平行線と線分の比 図形と相似 Try IT(トライイット)の平行線と線分の比の問題の様々な問題を解説した映像授業一覧ページです。平行線と線分の比 1 課 題 平行線の性質をもとにして、生徒たちが調べたこ とをそれぞれ生徒に説明(証明)させるという課題 学習である。生徒一人一人が自分で課題を設定し、 自分の力で証明していくのであるから、学習内容は 生徒によって異なる。三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内 FdData 中間期末ホームページ 掲載のpdf ファイル(サンプル)一覧 ※次のリンクはShiftキーをおし




平行線と線分の比 06 平行線と比の発展問題 その2 Youtube
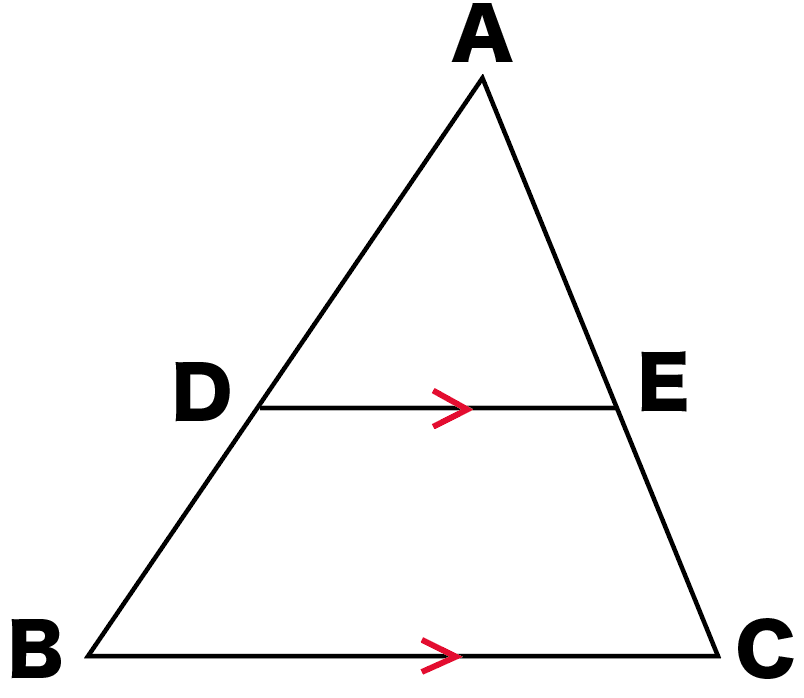



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく
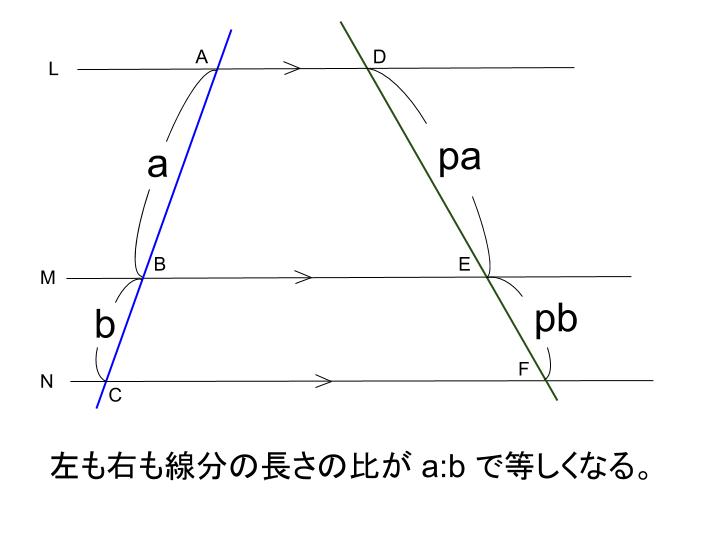
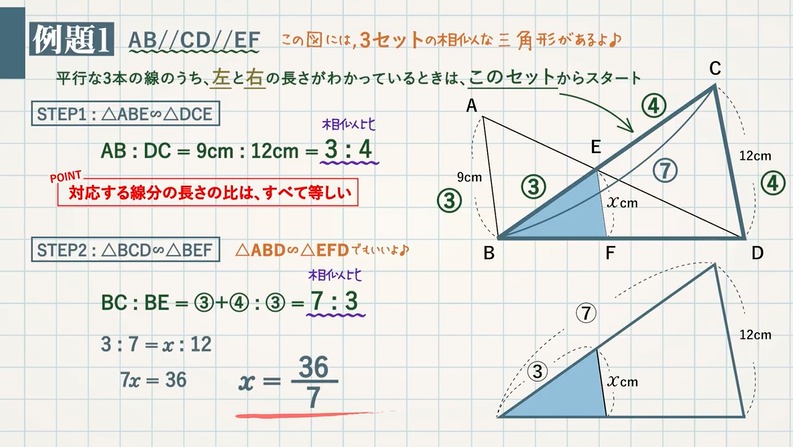
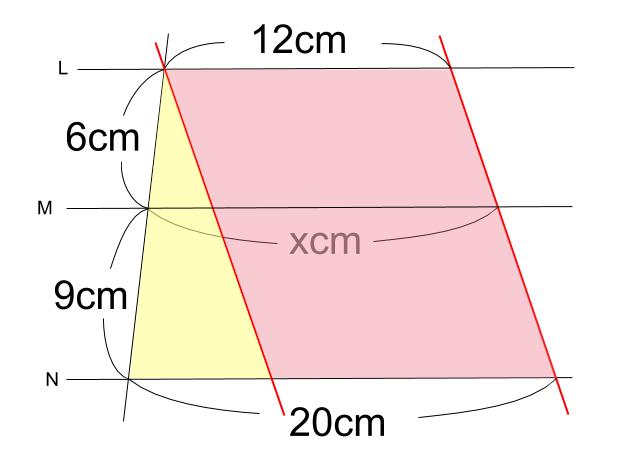
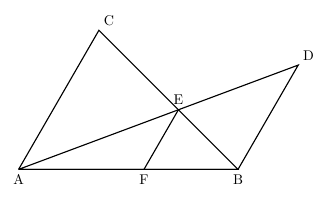
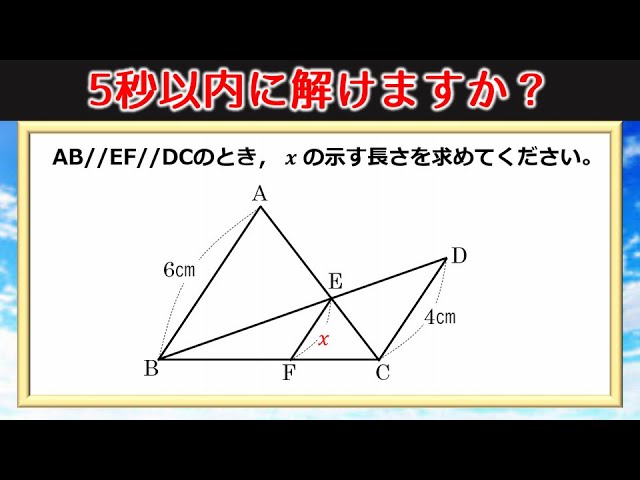
平行線と線分の比、線分の比と平行線って何が違うのですか?教えていだだけると助かります🙇♂️ 平行線と線分 とへabcで, 辺ab、ac の比 があるとき。 ⑯ pqzbc ならば, ap ab=aq ac=pq bc @ pq/bc ならば, ap pb=aq qc 簡分の比と平 上へabc で, 辺 ab、ac 上に, それぞれ, 原 があると平行線と線分の比の 性質を理解すること ができる。 5 単元計画(8時間) 次 時 学習活動・内容 生徒の思考 指導・援助の手だて 1 (1) 1 平行線と線分の比についての課題を見いだす。 (1) 実測できない線分の比について考える。 平行線 行線 れそうだぞ平行な $3$ 本の線のうち、左と右の長さがわかっているときは、$\rm ABE$ と $\rm DCE$ からスタート STEP $\textcolor{blue}{1}$ : $\textcolor{blue}{\rm ABE∽ DCE}$ $\rm ABDC=9cm12cm=\textcolor{blue}{34}$ (相似比) POINT:対応する線分の長さの比は、すべて等しい
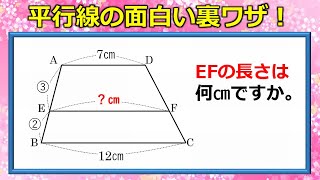



数学クイズ 気づけば数秒で解ける平行線の面白い裏ワザ Youtube




相似条件
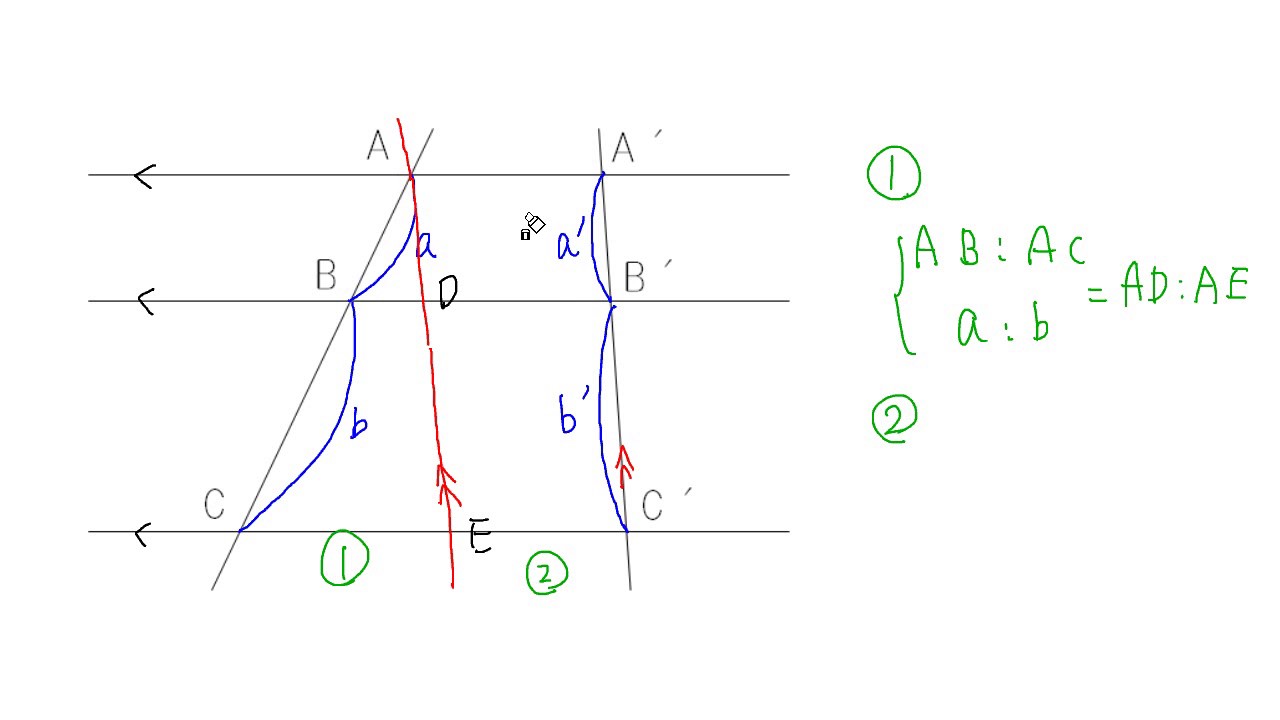
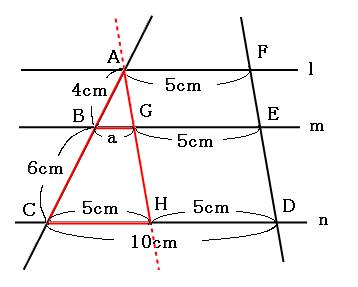
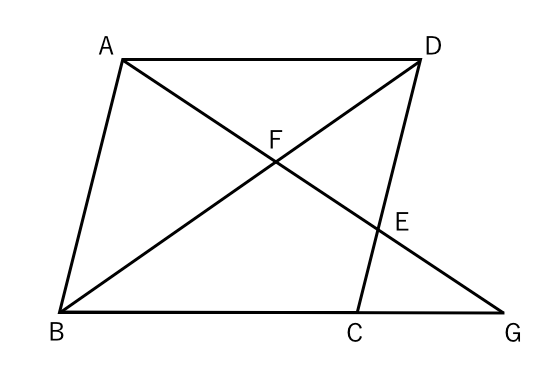
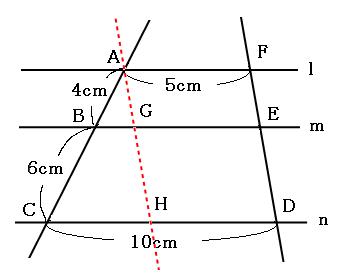
イ 平行線と線分の比の性質を使って、いろいろな線分の長さを求めることができる。 (2)指導の構想 ア 本時の課題の設定や問題解決の場面、まとめの場面において、生徒の考えや言葉を利用する ことで、自分の問題としての意識づけを図る。 イ 課題追究では、生徒同士の教え合いの場面を線分 bg と線分 ef との交点を h とするとき,線分 bh と線分 hg の長さの比を最も簡単な整数の比で表しなさい。 (神奈川県17年入試問題) 解説 やり直す 53 74 85 95 ** 円を含む・値を求める問題 ** 問題3 (選択肢の中から正しいものを1つクリック.解答すれば採点結果と解説が表示され3 平行線と線分の比 「平行線に直線が交わるとき、その交点の間の比は等しくなる」ことを次のように 証明した。直線l,m,nが平行であるとき、かっこに当てはまる語をうめよう。 点aを通り、直線a′に平行な直線を引き、それと直線m,nの交点をd,eとした。



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ
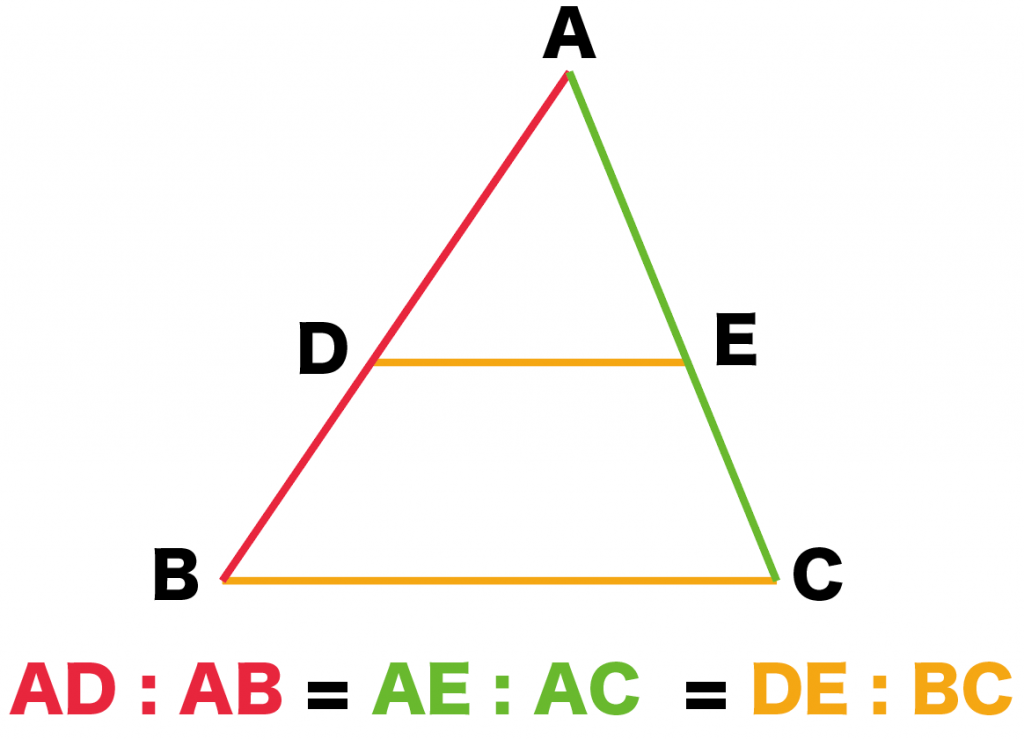
平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(l,m,n\) が平行 単元 平行線と比, 「 授業ノート🌸 見にくかったらごめんなさい🌐 ♡・コメント・フォロー 待ってます🗽🗽🗽」, 学年 中学3年生, キーワード 平行線と相似,平行線と線分の比,中点連結定理,相似比4 平行線と線分の比 平行な直線がある2つの三角形の線分の比について1 abc でpq¥bc のとき、 apq は abc と相似になる。 <証明> apq と abc において pq¥bc より、 平行線の同位角は等しいから ∠apq =∠abc ① ∠aqp =∠acb ② (∠a が共通も使えるけどね)



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
線分の比と平行線 次の定理を,線分の比と平行線の定理という。 線分の比と平行線 4abc の辺ab,ac 上の点をそれぞれp,q とするとき, 1 ap ab = aq ac ならば, pq // bc 2 ap pb = aq qc ならば, pq // bc b p a q c 対応する線分を間違えないように,自分で図平行線と線分の比 上の図3のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. bd//ce のとき まず図1の(1)が成り立つ. 前に習っているから,ここでは復習になるが一応証明しておくと次のように 線分比の移動の公式はよくわからないですが、「メネラウスの定理」は覚えておくべきでしょう。 今回は「適当な平行線を引いて」と書かれているのでそのやり方に則ってときましたが、メネラウスの定理を覚えていれば一発です。調べておいて損はないです。 2枚目の写真には平行線の線分比について載せました (知ってると思いますが)




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所
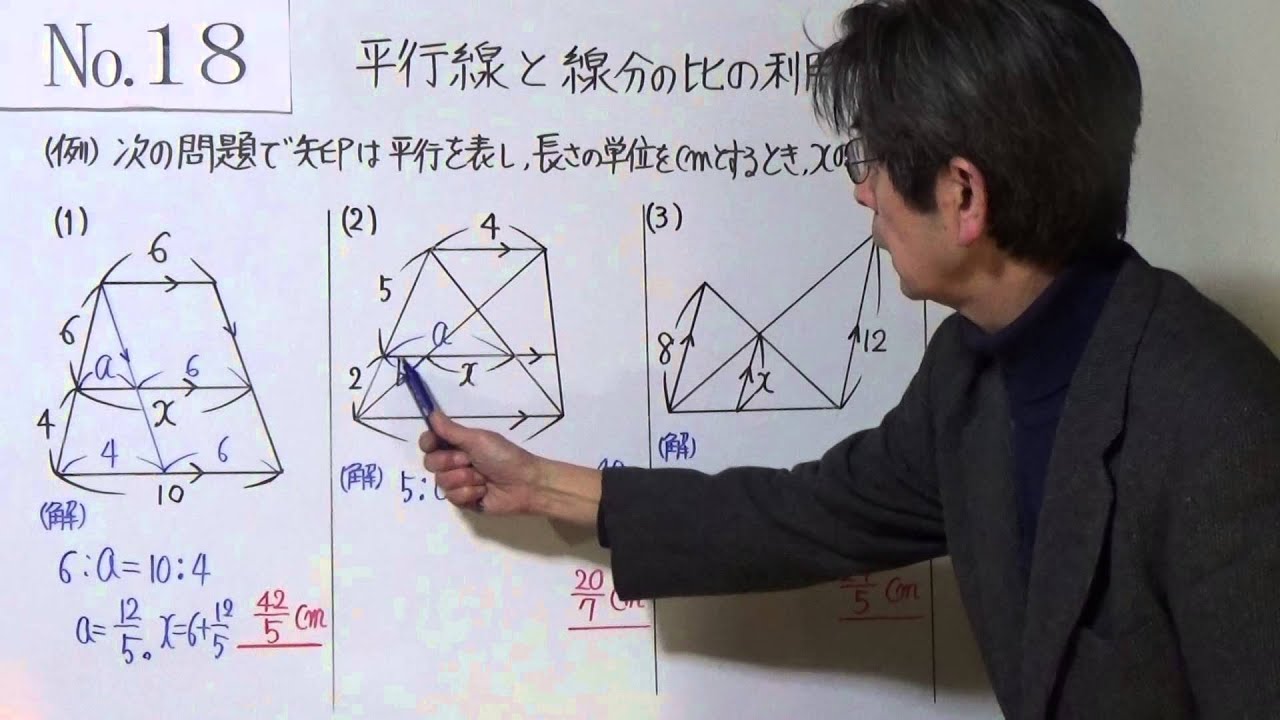



中3 18 5 平行線と線分の比の応用 Youtube




数学 相似の定理まとめ 中学生 数学のノート Clear
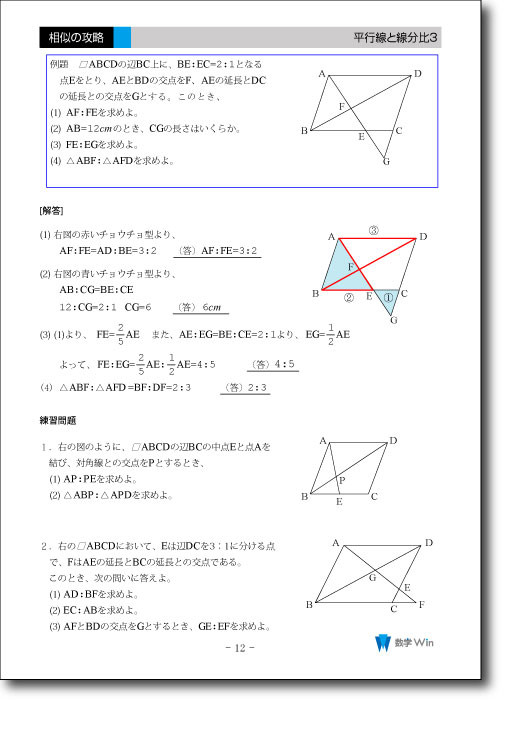



高校入試攻略シリーズ 相似の攻略 相似と計量 高校受験の数学攻略




中点連結定理の問題です の問題が分からないので 教えてください お願いします Clear



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に



禁断の裏技 メネラウスの定理 実演編 中学受験プロ講師ブログ
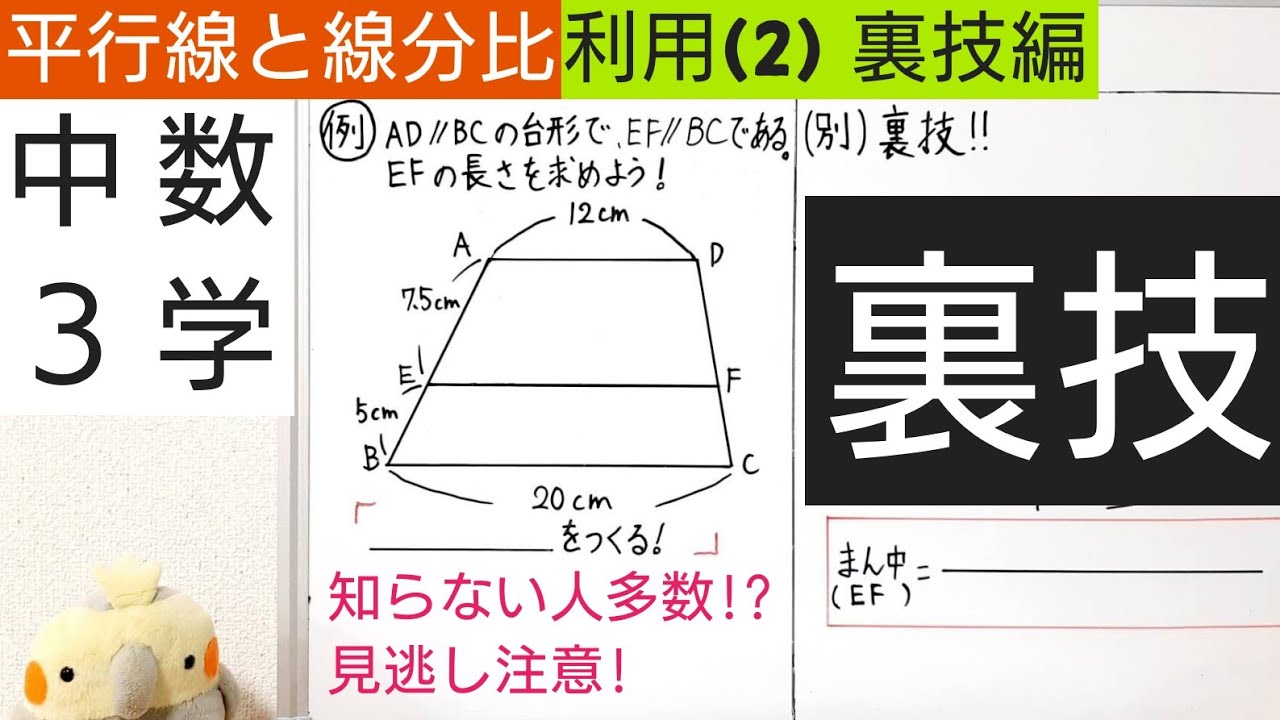



中3数学 15 平行線と線分の比の利用 2 裏技 Youtube



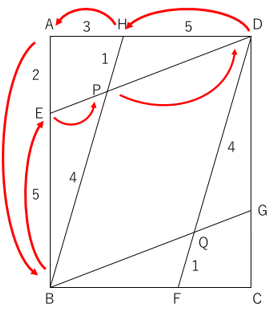
平行線と線分の比 辺の長さを求める応用問題4選 教遊者




中3数学 15 平行線と線分の比の利用 2 裏技 Youtube




角度の計算 裏技まとめ 教遊者




Amazon Co Jp 難関高校合格のための中学数学公式一覧 10秒で解けますか Ebook 夜早寝太郎 本
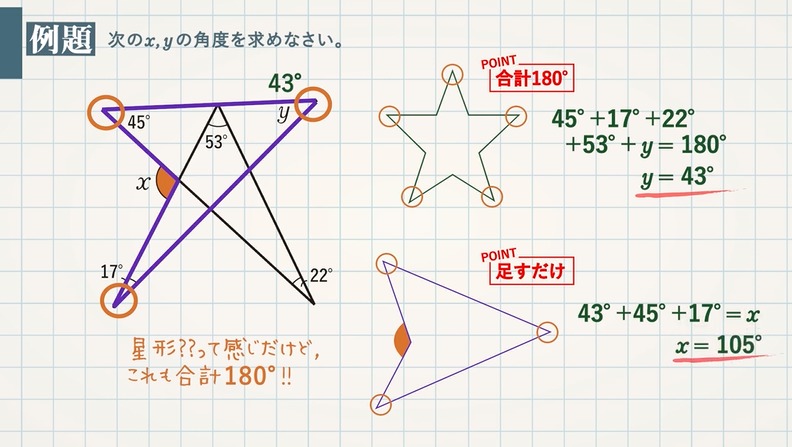



角度の計算 裏技まとめ 教遊者



中学校3年生の数学の授業
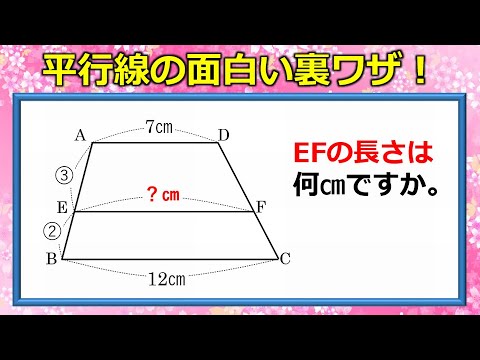



数学クイズ 気づけば数秒で解ける平行線の面白い裏ワザ Youtube



平行線と線分の比 Youtube




中3数学 15 平行線と線分の比の利用 2 裏技 Youtube



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



平行線と線分の比の裏技ってありますか Yahoo 知恵袋
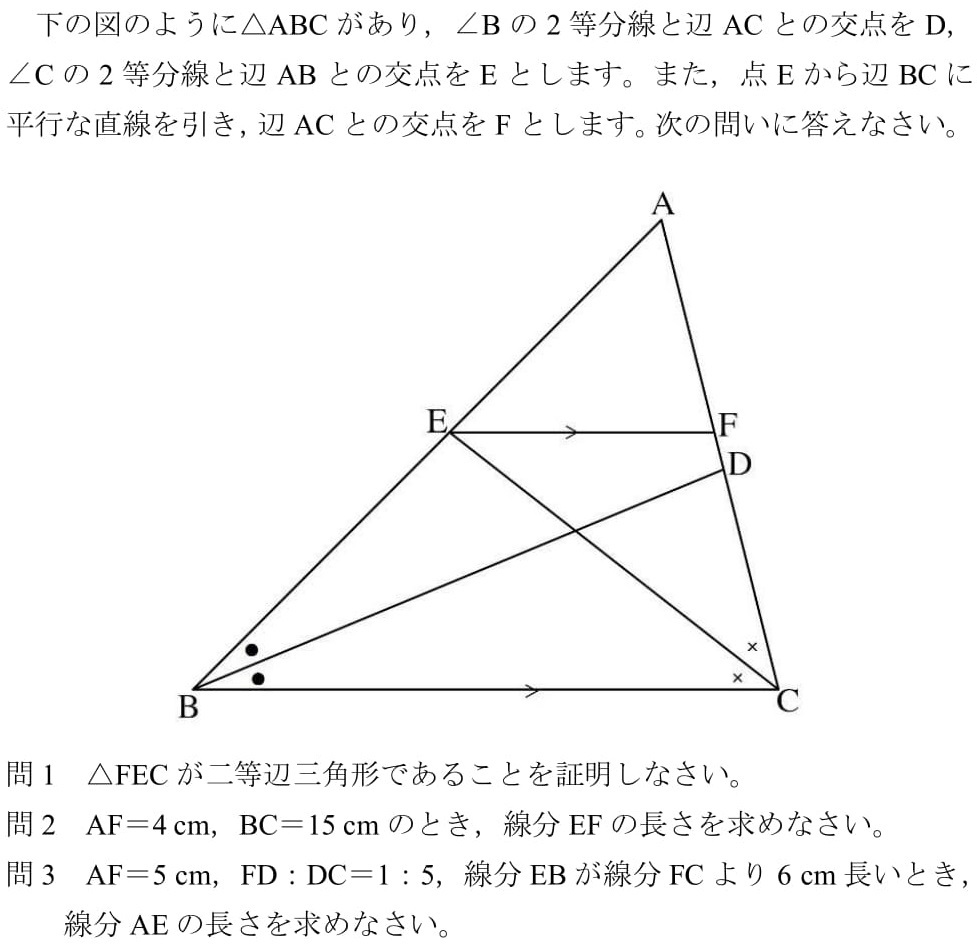



角の2等分線超難問 いつかの大分県 高校入試 数学 良問 難問



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所




平行線と比の利用 チーム エン




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所
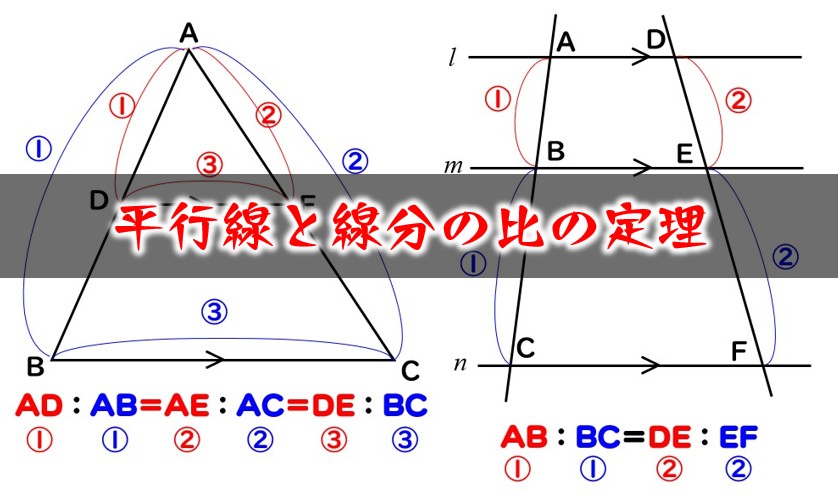



平行線と線分の比の定理 の問題の解き方 数学fun



Zckzah2254agba360j34p3p4a5h4c Net Tips 8




2回とも中点連結定理を使える時と1回しか使えないときの違いを教えてください Clear
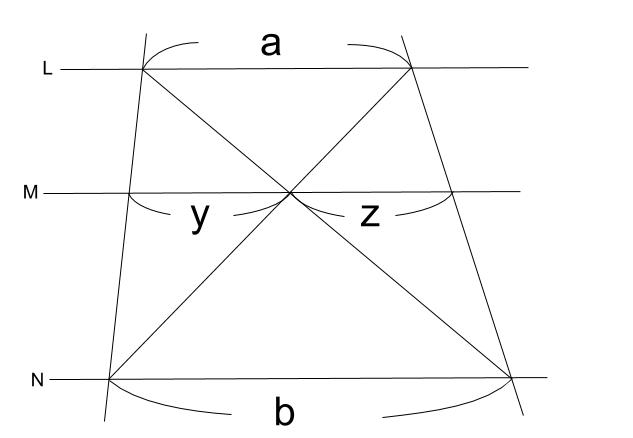



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor
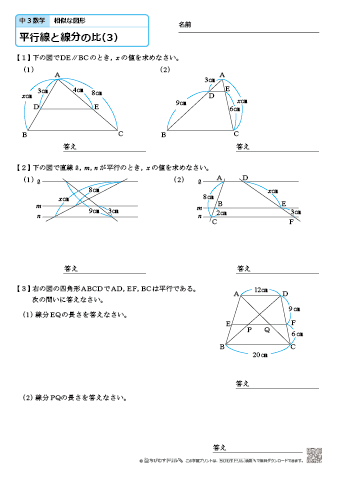



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中学校3年生の数学の授業




中3数学 平行線と比3 平行 線分比 練習編 映像授業のtry It トライイット
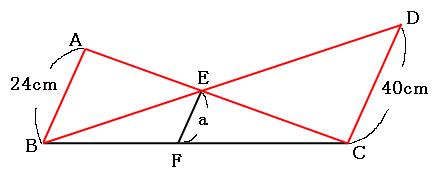



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ
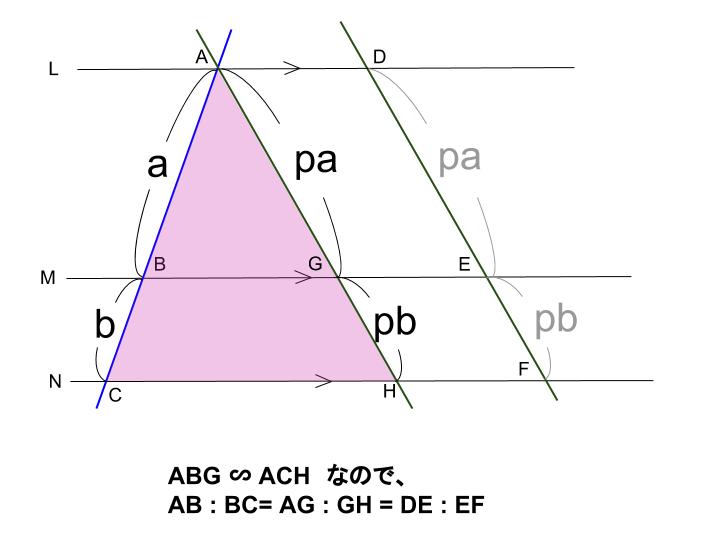



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su



1




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所




中3 差がつく 裏技 高校受験のための数学の定理まとめ 中学生 数学のノート Clear




中3 数学lll 平行線と線分の比 中学生 数学のノート Clear




中学受験 算数 展開図 最強ルールと決まりを使って攻略 中学受験アンサー




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
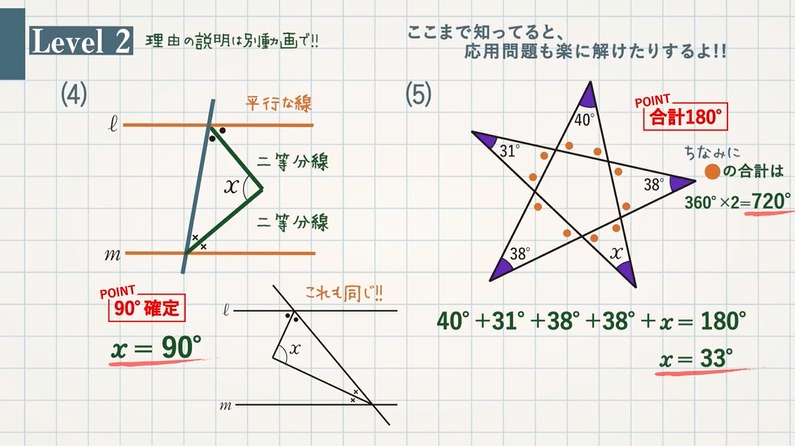



角度の計算 裏技まとめ 教遊者
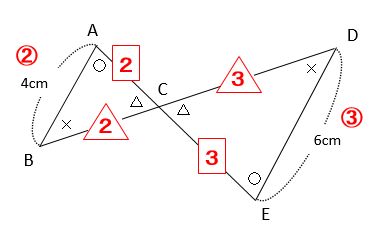



相似 平行線と三角形の問題ではちょうちょかピラミッドを探せ みみずく戦略室



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




高校数学a 線分の内分点と外分点の図示 受験の月



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に



1



平行線の線分比の問題の解法 夢を叶える塾



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




三角形の線分比を一瞬で出す裏ワザ Comken Youtube



1




相似 裏ワザ公式の使い方を解説 Youtube
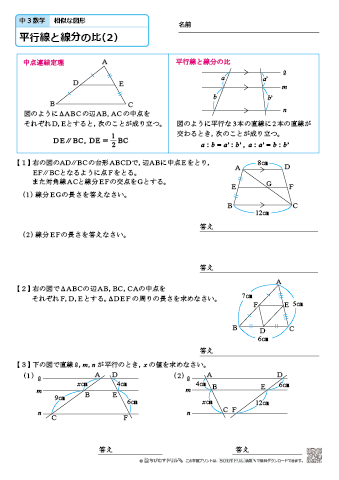



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




中3 数学lll 平行線と線分の比 中学生 数学のノート Clear



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の利用 中3数学 Youtube




数学 中3 49 平行線と線分の比 基本編 Youtube



図形問題 知っている人は5秒で解ける相似の裏技 Youtube



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし




中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
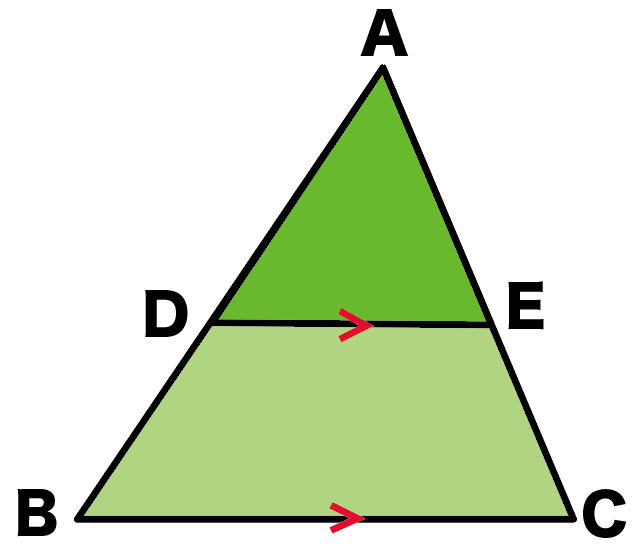



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




急ぎです 答えは15です 考え方 式を教えてください Clear




平行線と線分の比 三角形の比の取り方を簡単な問題で覚えよう 中学や高校の数学の計算問題




中3数学 15 平行線と線分の比の利用 1 裏技 Youtube



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法



Q Tbn And9gcs8yek Ytk4aevkupzlfiomyr1swah7y0fxr8n2 Yhcmpzyumt Usqp Cau




中3 数学lll 平行線と線分の比 中学生 数学のノート Clear



中3数学 15 平行線と線分の比の利用 2 裏技 Youtube




中3 数学 相似 基本 証明 中学生 数学のノート Clear




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所
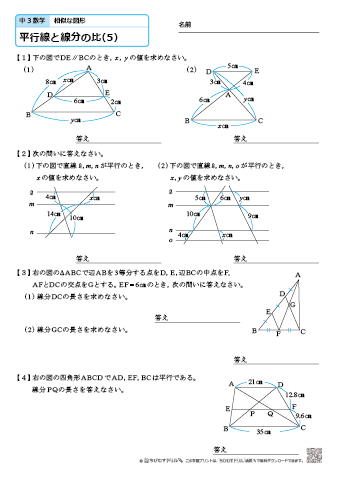



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




角度の計算 裏技まとめ 教遊者
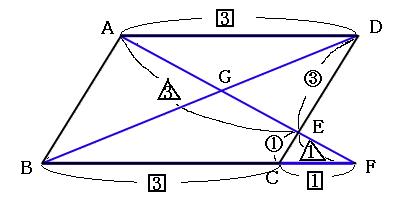



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ




高校数学a メネラウスの定理とその逆の証明 受験の月
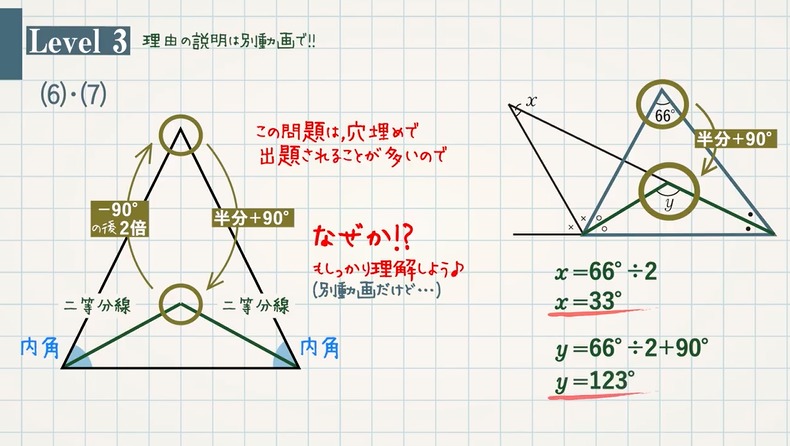



角度の計算 裏技まとめ 教遊者
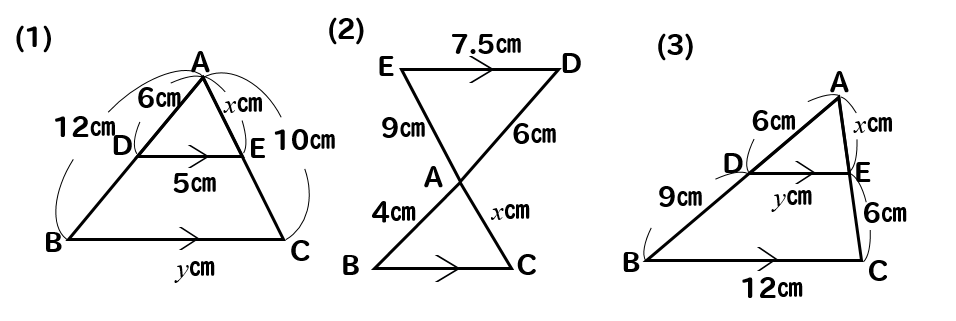



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
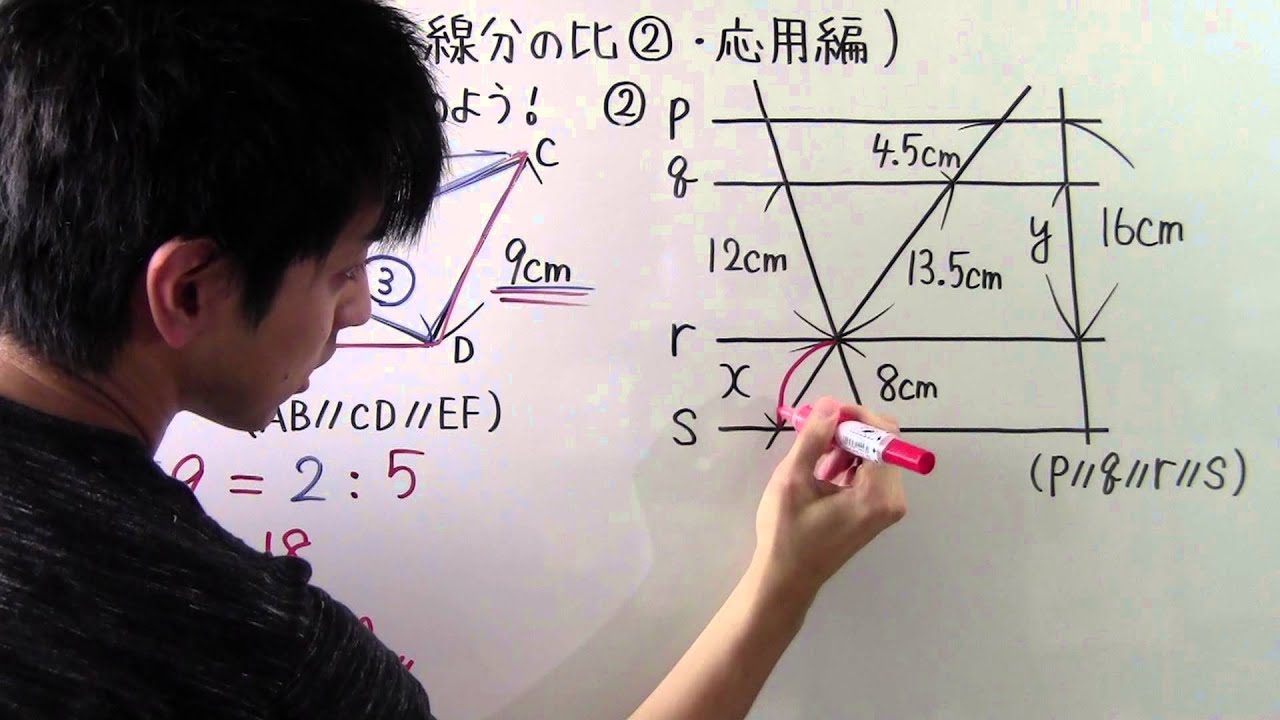



数学 中3 50 平行線と線分の比 応用編 Youtube



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
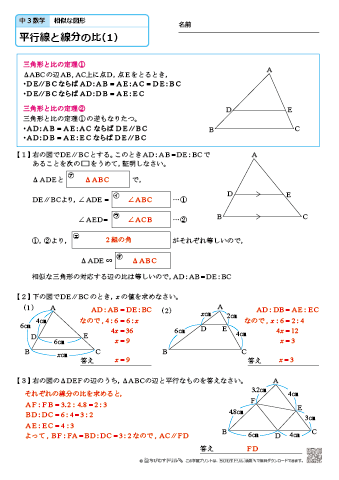



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




平行線と線分の比 辺の長さを求める応用問題4選 教遊者




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



Studydoctor平行線と台形 中3数学 Studydoctor



0 件のコメント:
コメントを投稿