教科書レベルの問題一覧と解答 数学a 図形の性質 教科書より詳しい高校数学
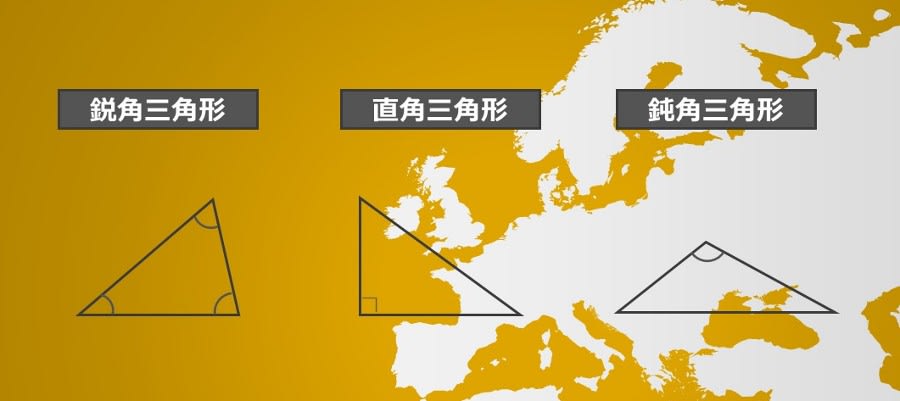
90 定理 平行于三角形一边的直线和其他两边(或两 边的延长线)相交,所构成的三角形与原三角形相似 91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA) 92 直角三角形被斜边 三角形的定理很多:1三角形内角和等于180度。 2三角形的任何两边的和一定大于第三边 ,由此亦可证明得三角形的任意两边的差一定小于第三边。 3勾股定理:直角三角形两直角边的
三角形 定理 一覧 高校
三角形 定理 一覧 高校- 1つの三角形において 大きい辺に向かい合う角は,小さい辺に向かい合う各より大きい。 大きい角に向かい合う辺は,小さい角に向かい合う辺より大きい。 すなわち AB < AC ⇔∠C三角関数 編集 最も基本的な関数は正弦関数(サイン、sine)と余弦関数(コサイン、cosine)である。 これらは sin (θ), cos (θ) または 括弧 を略して sin θ, cos θ と記述される( θ は対象となる角

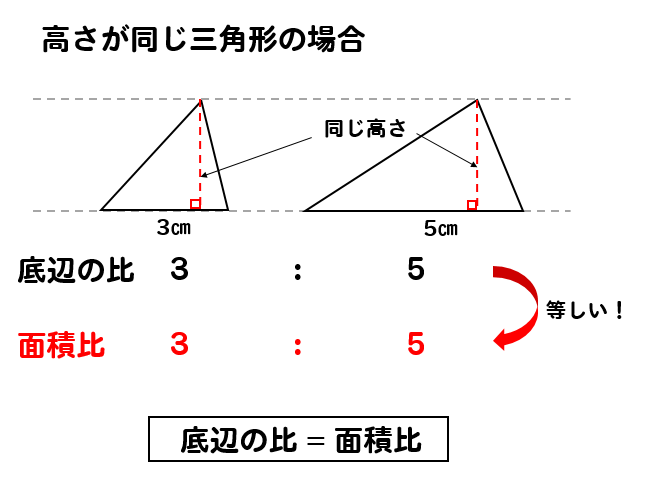
ある2つの三角形の辺の比と面積比について 身勝手な主張
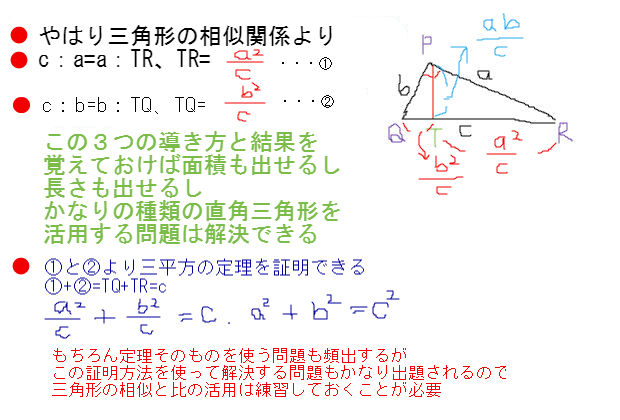
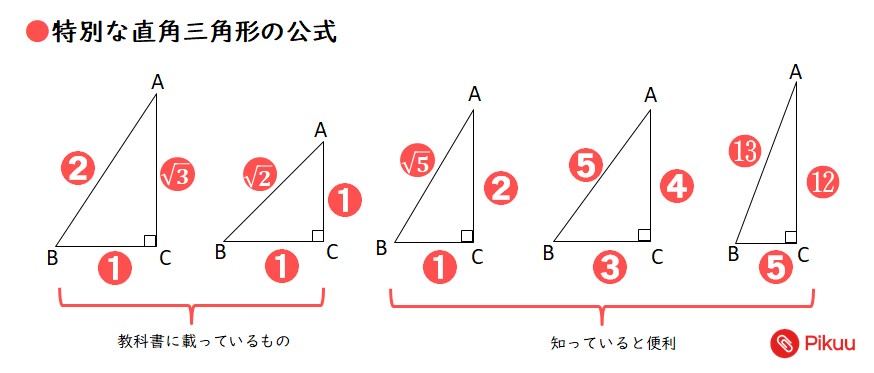
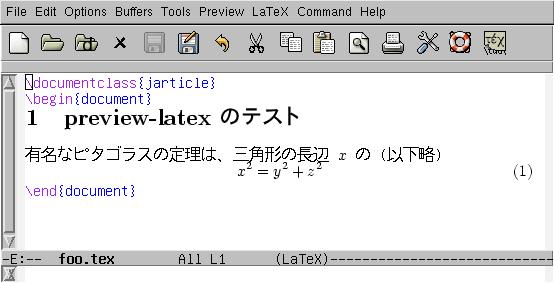
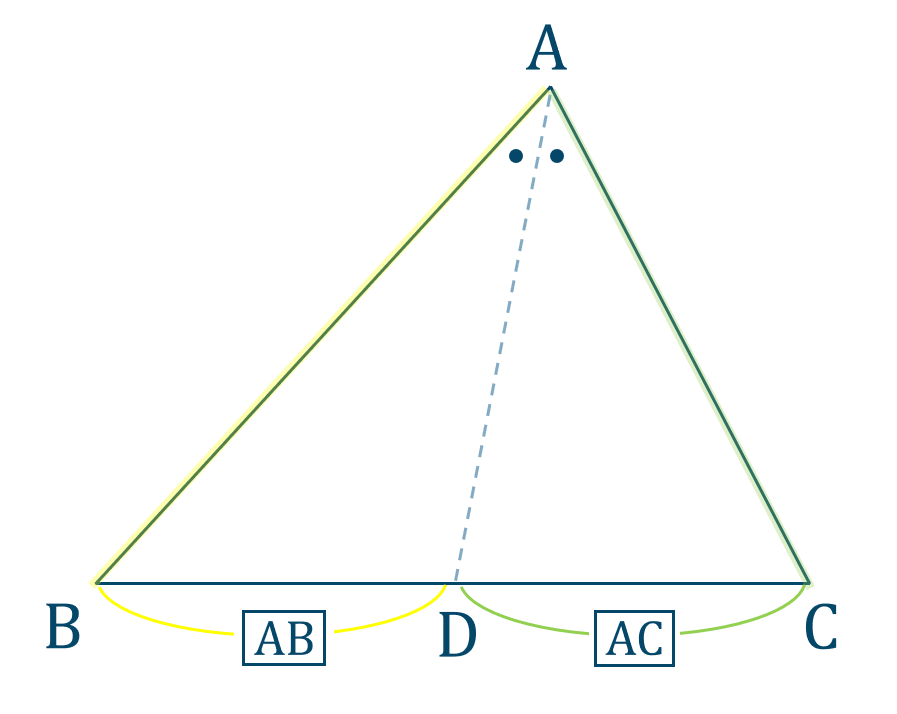
三角形と比の定理 A B C D E ABCの辺AB,AC上の点をそれぞれD, Eとするとき、 ①DE//BCならADAB=AEAC=DEBCである。 ②DE//BCならADDB=AEECである。 ※この定理はD, Eが辺BA, CA 高校受験に向けた、中学生の数学で苦手意識をいだきやすいのは証明 証明に用いる定義や定理は、 2年生で習ってたり、3年生で習っていたりしてうろ覚えのものもあるので 一覧を直角三角形と三角関数 三平方の定理(ピタゴラスの定理) 三平方の定理(ピタゴラスの定理) 直角三角形において, a^2b^2=c^2 a2 b2 = c2 つまり「斜辺以外の二辺の長さの二乗の和」は「斜辺
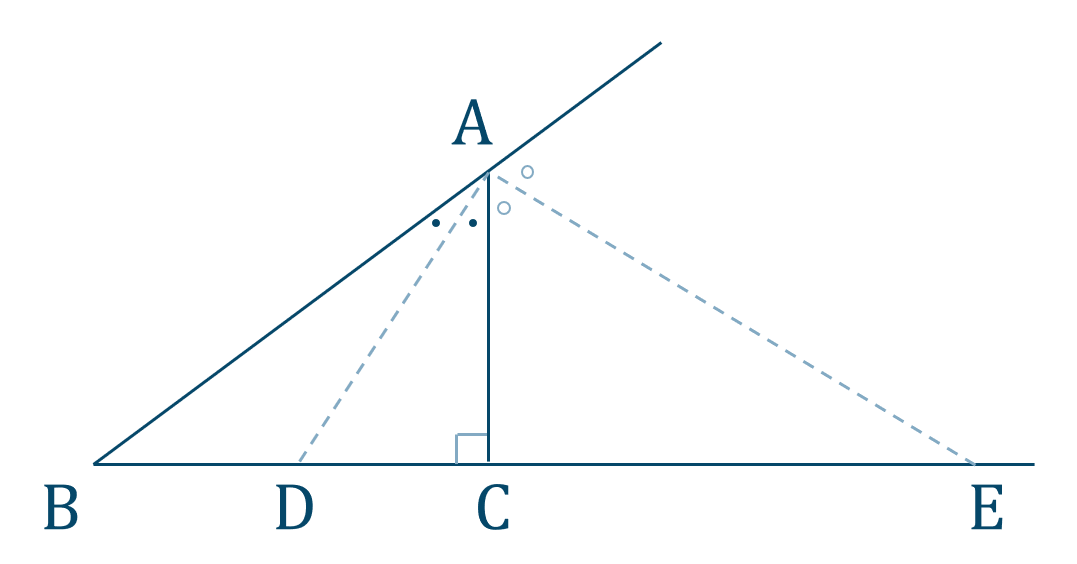
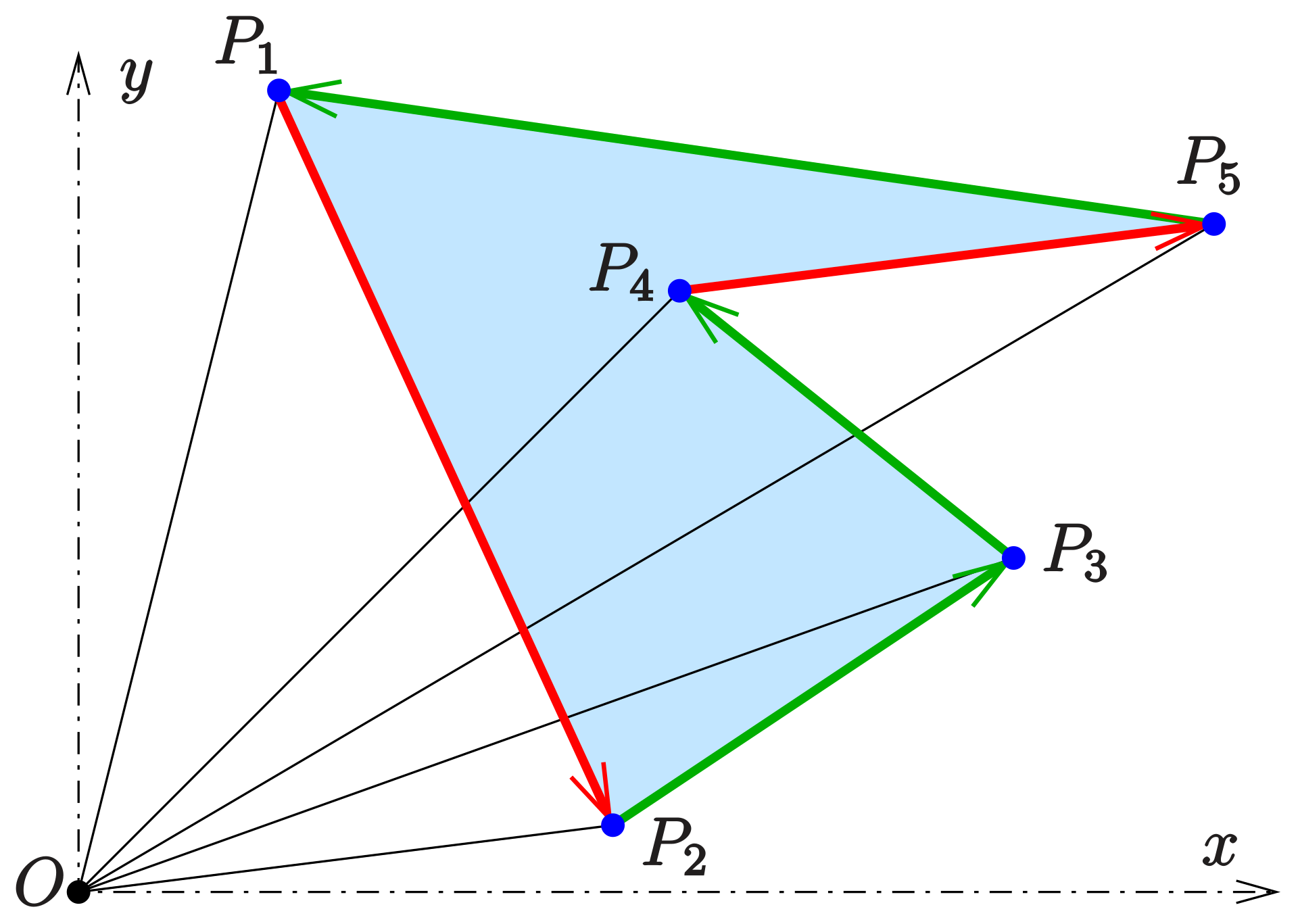
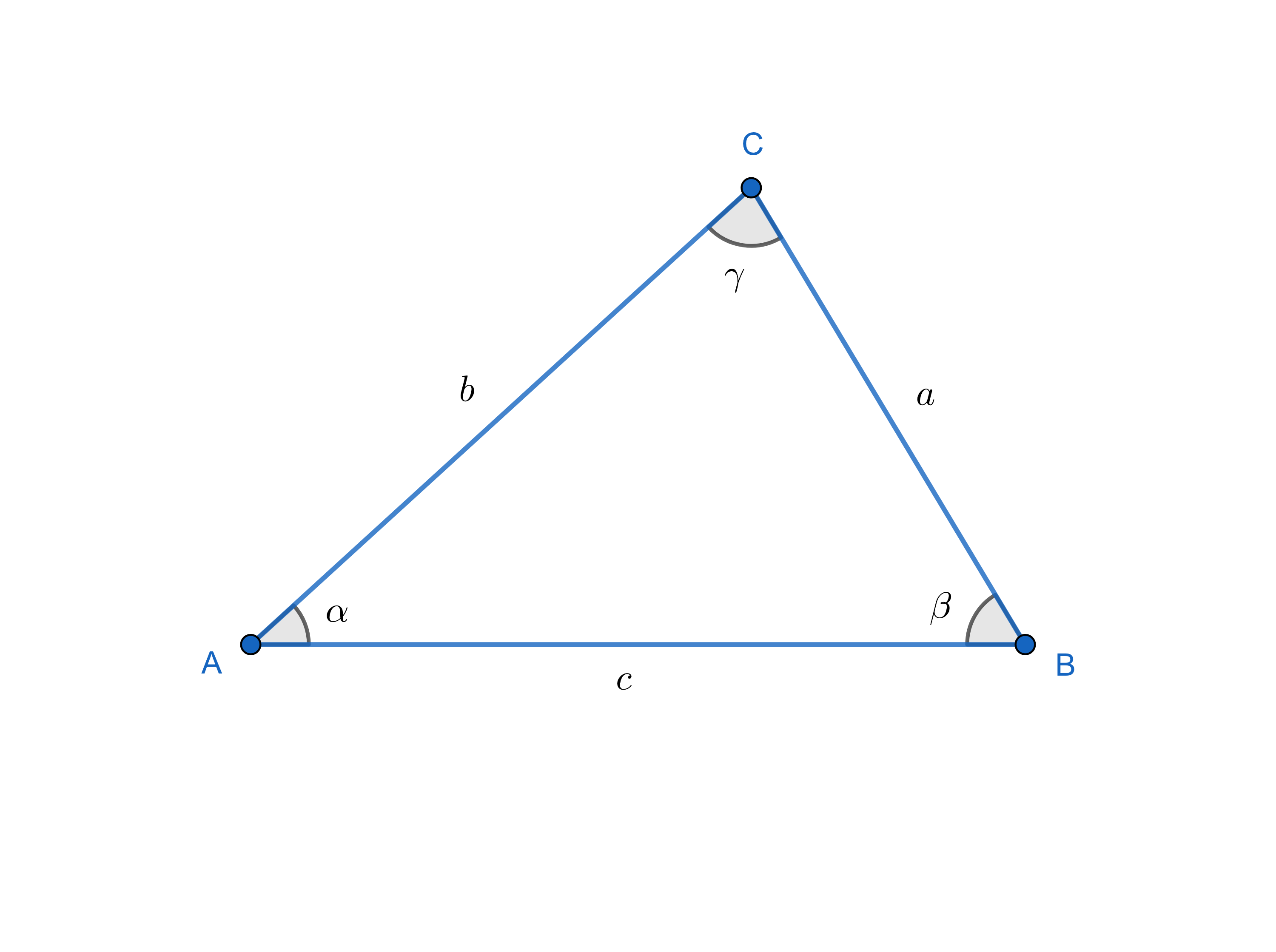
余弦定理は 「三角形のある角 (のcos)と、三角形を形成する各辺の間に成り立っている関係式」 のことを指しています。 実際に図を見ながらイメージしてみましょう。 図1のように三 三角比の基本 三角定規に用いられる、 30°・45°・60°の三角比 が基本となります。 これらは高校数学でよく用いられるので、必ず覚えましょう。 30°の三角比 45°の三角比 60°の三角Cot (コタンジェント)を変換 三角形の計算 ・ 正三角形 (辺から高さと面積) ・ 正三角形 (高さから辺と面積) ・ 正三角形 (面積から辺と高さ) ・ 直角三角形 (底辺と高さ) ・ 直角三角形 (底辺と斜辺)
三角形 定理 一覧 高校のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
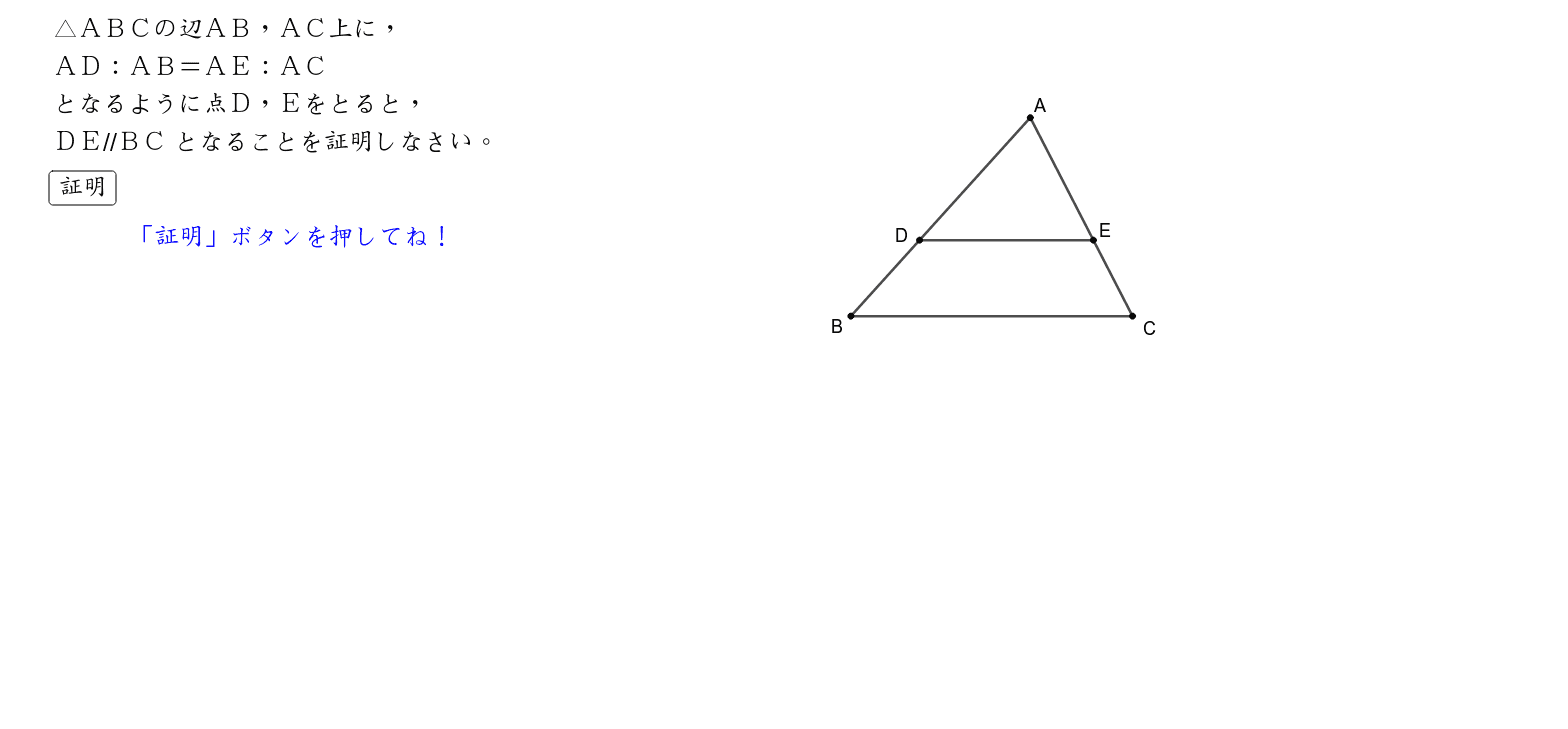 |  |  |
 |  | |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 定理 一覧 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
二等辺三角形の定理は 「二等辺三角形の頂角の二等分線は、 底辺を垂直に2等分する。」 正三角形の定義は 「3辺が等しい三角形」 正三角形の定理は 「正三角形の3つの角は等しい」 三角形の定理 一般三角形的余弦定理 假设我们将三角形ABC的三条边看作向量,其中向量a和向量b的夹角即为角C,向量c为a、b之差 将上述等式平方可得 因为三条边可以任意组合,同理证明可得 此三个等式就是三角形中的余弦定理,它的意义是一个边长可以表示成另外两个
Incoming Term: 三角形 定理 一覧, 三角形 定理 一覧 中学, 三角形 定理 一覧 高校,




0 件のコメント:
コメントを投稿